题目内容
20. 如图所示,一个被x轴与曲线方程y=0.2sin$\frac{10π}{3}$x(m)所围的空间存在着匀强磁场.磁场方向垂直纸面向里,磁感应强度B=0.2T.正方形金属线框的边长是L=0.2m,电阻是R=0.1Ω,它的一边与x轴重合,在拉力F的作用下,以v=10m/s的速度水平向右匀速运动.求:
如图所示,一个被x轴与曲线方程y=0.2sin$\frac{10π}{3}$x(m)所围的空间存在着匀强磁场.磁场方向垂直纸面向里,磁感应强度B=0.2T.正方形金属线框的边长是L=0.2m,电阻是R=0.1Ω,它的一边与x轴重合,在拉力F的作用下,以v=10m/s的速度水平向右匀速运动.求:(1)线圈中电流的最大值.
(2)把线框拉过磁场区的过程中产生了多少焦耳热?
分析 (1)线框的一边做切割磁感线运动,产生感应电动势,当切割长度最大时,感应电流最大,根据电磁感应知识求解;
(2)线框右边和左边分别切割磁感线,产生正弦式交变电流,可用切割感应电动势公式、安培力和功知识求解功,再由能量守恒定律求解焦耳热.
解答 解:(1)当线框的一条竖直边运动到x=0.15m处时,线圈的感应电动势最大,感应电动势的最大值:
Em=BLv=0.2×0.2×10V=0.4V,
电路最大电流:Im=$\frac{{E}_{m}}{R}$=$\frac{0.4}{0.1}$=4A,
(2)把线框拉过磁场区域时,因为有效切割长度是按正弦规律变化的,线框中的电流也是按正弦规律变化的(有一段时间线框中没有电流).电动势的有效值是:
E=$\frac{{E}_{m}}{\sqrt{2}}$=$\frac{0.4}{\sqrt{2}}$=0.2$\sqrt{2}$V,
从图示位置开始把线框右边拉至x=0.15m坐标处需要的时间:
t=$\frac{x}{v}$=$\frac{0.3}{10}$=0.03s,
拉力做功:W=$\frac{{E}^{2}}{R}$t=$\frac{(0.2\sqrt{2})^{2}}{0.1}×0.03$=0.024J,
根据能量守恒定律可知,拉力做功转化为回路中产生的焦耳热,故产生的焦耳热为0.024J;
答:(1)线圈中电流的最大值为4A.
(2)把线框拉过磁场区的过程中产生了0.024J的焦耳热.
点评 本题要注意是线框中产生的是正弦式电流,求电功要用电动势的有效值,正弦式电流的最大值是有效值的$\sqrt{2}$倍.

练习册系列答案
相关题目
8. 如图所示,为两个质点A、B在同一条直线上运动的速度图象,A、B同时从同地开始运动,下列说法中正确的是( )
如图所示,为两个质点A、B在同一条直线上运动的速度图象,A、B同时从同地开始运动,下列说法中正确的是( )
 如图所示,为两个质点A、B在同一条直线上运动的速度图象,A、B同时从同地开始运动,下列说法中正确的是( )
如图所示,为两个质点A、B在同一条直线上运动的速度图象,A、B同时从同地开始运动,下列说法中正确的是( )| A. | A和B沿不同方向运动 | B. | A的加速度大于B的加速度 | ||
| C. | t1时刻A、B两物体速度相等 | D. | t1时刻A、B两物体相遇 |
15. 在“探究小车速度随时间变化的规律”的实验中,打点计时器使用的交流电的频率为50Hz,记录小车运动的纸带如图10所示.在纸带上选择0、1、2、3、4、5共6个计数点,相邻两计数点之间还有四个点未画出.纸带旁并排放着带有最小分度为毫米的刻度尺,零刻度线跟“0”计数点对齐.由图可以读出三个计数点1、3、5跟0点的距离填入下列表格中.
在“探究小车速度随时间变化的规律”的实验中,打点计时器使用的交流电的频率为50Hz,记录小车运动的纸带如图10所示.在纸带上选择0、1、2、3、4、5共6个计数点,相邻两计数点之间还有四个点未画出.纸带旁并排放着带有最小分度为毫米的刻度尺,零刻度线跟“0”计数点对齐.由图可以读出三个计数点1、3、5跟0点的距离填入下列表格中.
计算小车通过计数点“2”的瞬时速度公式为v2=$\frac{{{d_2}-{d_1}}}{2T}$(以d1、d2及相邻计数点间时间T来表示)代入得v2=0.21m/s.(结果保留两位有效数字)
 在“探究小车速度随时间变化的规律”的实验中,打点计时器使用的交流电的频率为50Hz,记录小车运动的纸带如图10所示.在纸带上选择0、1、2、3、4、5共6个计数点,相邻两计数点之间还有四个点未画出.纸带旁并排放着带有最小分度为毫米的刻度尺,零刻度线跟“0”计数点对齐.由图可以读出三个计数点1、3、5跟0点的距离填入下列表格中.
在“探究小车速度随时间变化的规律”的实验中,打点计时器使用的交流电的频率为50Hz,记录小车运动的纸带如图10所示.在纸带上选择0、1、2、3、4、5共6个计数点,相邻两计数点之间还有四个点未画出.纸带旁并排放着带有最小分度为毫米的刻度尺,零刻度线跟“0”计数点对齐.由图可以读出三个计数点1、3、5跟0点的距离填入下列表格中.| 距离 | d1 | d2 | d3 |
| 测量值/cm | 1.20 | 5.40 | 12.02 |
12.下列说法正确的是( )
| A. | 开普勒通过观察天象以及深入研究第谷的数据提出行星运动三大定律 | |
| B. | 相对论和量子力学的出现,使经典力学失去了意义 | |
| C. | 第三宇宙速度达到16.7 km/s,已经超出了经典力学的使用范围 | |
| D. | 牛顿是经典力学的奠基人,他提出了牛顿运动定律与万有引力定律 |
9. 如图所示,竖直金属板A、B间电压为U0,板中央有小孔O和O1,现有足够多的同种粒子源源不断地从小孔O进入金属板A、B间,并被加速后从O1进入右侧水平平行金属板C、D间,O1O2是极板C、D的中线,金属板C、D的长与板间距相等,两板间电压U可调,不计粒子重力及进入O孔时的初速度,所有粒子均不能打在极板上,则U与U0应满足( )
如图所示,竖直金属板A、B间电压为U0,板中央有小孔O和O1,现有足够多的同种粒子源源不断地从小孔O进入金属板A、B间,并被加速后从O1进入右侧水平平行金属板C、D间,O1O2是极板C、D的中线,金属板C、D的长与板间距相等,两板间电压U可调,不计粒子重力及进入O孔时的初速度,所有粒子均不能打在极板上,则U与U0应满足( )
 如图所示,竖直金属板A、B间电压为U0,板中央有小孔O和O1,现有足够多的同种粒子源源不断地从小孔O进入金属板A、B间,并被加速后从O1进入右侧水平平行金属板C、D间,O1O2是极板C、D的中线,金属板C、D的长与板间距相等,两板间电压U可调,不计粒子重力及进入O孔时的初速度,所有粒子均不能打在极板上,则U与U0应满足( )
如图所示,竖直金属板A、B间电压为U0,板中央有小孔O和O1,现有足够多的同种粒子源源不断地从小孔O进入金属板A、B间,并被加速后从O1进入右侧水平平行金属板C、D间,O1O2是极板C、D的中线,金属板C、D的长与板间距相等,两板间电压U可调,不计粒子重力及进入O孔时的初速度,所有粒子均不能打在极板上,则U与U0应满足( )| A. | U>U0 | |
| B. | U<2U0 | |
| C. | U>2U0 | |
| D. | 因不知极板C、D的长,所以无法确定U和U0的关系 |
10. 歼20战斗机为中国人民解放军研制的第四代战机.如图所示,机身长为l,机翼两端点C、D的距离为d,现该战斗机在我国近海海域上空以速度v沿水平方向飞行,已知战斗机所在空间地磁场磁感应强度的竖直分量大小为B,C、D两点间的电势差为U.则( )
歼20战斗机为中国人民解放军研制的第四代战机.如图所示,机身长为l,机翼两端点C、D的距离为d,现该战斗机在我国近海海域上空以速度v沿水平方向飞行,已知战斗机所在空间地磁场磁感应强度的竖直分量大小为B,C、D两点间的电势差为U.则( )
 歼20战斗机为中国人民解放军研制的第四代战机.如图所示,机身长为l,机翼两端点C、D的距离为d,现该战斗机在我国近海海域上空以速度v沿水平方向飞行,已知战斗机所在空间地磁场磁感应强度的竖直分量大小为B,C、D两点间的电势差为U.则( )
歼20战斗机为中国人民解放军研制的第四代战机.如图所示,机身长为l,机翼两端点C、D的距离为d,现该战斗机在我国近海海域上空以速度v沿水平方向飞行,已知战斗机所在空间地磁场磁感应强度的竖直分量大小为B,C、D两点间的电势差为U.则( )| A. | U=Blv,C点电势高于D点电势 | B. | U=Blv,D点电势高于C点电势 | ||
| C. | U=Bdv,C点电势高于D点电势 | D. | U=Bdv,D点电势高于C点电势 |
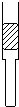 如图所示,一根上粗下细(上下两段各自粗细均匀)的玻璃管上端开口、下端封闭,上端足够长,下端有一段水银柱封闭了一定质量的理想气体.现将封闭气体温度同时缓慢降低,在气体温度不断下降过程中,水银柱缓慢向下移动,则下图中的图线最接近被封闭气体体积V和热力学温度T关系的是( )
如图所示,一根上粗下细(上下两段各自粗细均匀)的玻璃管上端开口、下端封闭,上端足够长,下端有一段水银柱封闭了一定质量的理想气体.现将封闭气体温度同时缓慢降低,在气体温度不断下降过程中,水银柱缓慢向下移动,则下图中的图线最接近被封闭气体体积V和热力学温度T关系的是( )



 如图所示,在同一竖直平面内有一个半径为r的四分之一光滑圆弧和一半径为R=2r的光滑圆轨道通过平滑小孔连接,小球可以无能量损失地切入圆轨道内,今有两个可视为质点的质量为m的小球A和B,B球位于圆轨道的最低点,现让球A在圆弧开口的正上方h高处由静止释放后恰好进入四分之一光滑圆弧中,随后从小孔进入大圆轨道与B球碰撞并粘合在一起,欲使A球在碰撞前后都能在大圆轨道中做完整的圆运动,试求h的最小高度.
如图所示,在同一竖直平面内有一个半径为r的四分之一光滑圆弧和一半径为R=2r的光滑圆轨道通过平滑小孔连接,小球可以无能量损失地切入圆轨道内,今有两个可视为质点的质量为m的小球A和B,B球位于圆轨道的最低点,现让球A在圆弧开口的正上方h高处由静止释放后恰好进入四分之一光滑圆弧中,随后从小孔进入大圆轨道与B球碰撞并粘合在一起,欲使A球在碰撞前后都能在大圆轨道中做完整的圆运动,试求h的最小高度. 水平放置的导体框架,宽L=0.50m,接有电阻R=0.20Ω,匀强磁场垂直框架平面向里,磁感应强度B=0.40T.一导体棒ab垂直框边跨放在框架上,并能无摩擦地在框架上滑动,框架和导体ab的电阻均不计.当ab以v=4.0m/s的速度向右匀速滑动时,求:
水平放置的导体框架,宽L=0.50m,接有电阻R=0.20Ω,匀强磁场垂直框架平面向里,磁感应强度B=0.40T.一导体棒ab垂直框边跨放在框架上,并能无摩擦地在框架上滑动,框架和导体ab的电阻均不计.当ab以v=4.0m/s的速度向右匀速滑动时,求: