Question

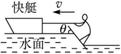
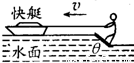
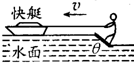在电视节目中我们常常能看到一种精彩的水上运动--滑水板，如图所示．运动员在快艇的水平牵引力作用下，脚踏倾斜滑板在水上匀速滑行，设滑板是光滑的．若运动员与滑板的总质量为m=70kg，滑板的总面积为S=0.12m²，水的密度为ρ=1.0×10³ kg/m³．理论研究表明：当滑板与水平方向的夹角（板前端抬起的角度）为θ时，水对板的作用力大小为N=ρSv²sin²θ，方向垂直于板面．式中v为快艇的牵引速度，S为滑板的滑水面积，求为了使滑板能在水面上滑行，快艇水平牵引滑板的最小速度．

Answer 1

分析：根据力的平衡求出速度和滑板与水平方向的夹角的关系，根据数学知识导数求该表达式的最小值，从而得出最小速度．

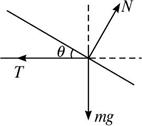
解答：解：滑板和运动员受重力mg、水对滑板的弹力N，绳子的拉力F，不计水的阻力，根据物体的平衡有：
Ncosθ-mg=0
又根据题设条件，N=ρSv²sin²θ，可得牵引的速度v=

mg ρSsin2θcosθ

在mg、ρ、S一定的条件下，v是θ的函数，当θ取一定值时，v有最小值．设y=sin²θcosθ，则当y有最大值时，v有最小值．求y的导数并令其为零．

dy

dθ

=2sinθcos2θ-sin3θ=0 解得，tanθ=

2

．
根据数学三角函数得，cosθ=

3

3

，sin2θ=

2

3

则ymax=

2 3

9

代入速度表达式中，最小速度v=

3 3 mg 2ρS

=3.9m/s．
故快艇水平牵引滑板的最小速度为3.9m/s．

点评：本题本来是一道相当难的问题，数学计算较复杂，但使用导数运算后，使的一难题变为一道常规题．