题目内容
2.工业生产中需要物料配比的地方,常用“吊斗式”电子秤,图1所示的是“吊斗式”电子秤的结构图,其中实现称质量的关键性元件是拉力传感器.拉力传感器的内部电路如图2所示,R1、R2、R3是定值电阻,R1=20kΩ,R2=10kΩ,R0是对拉力敏感的应变片电阻,其电阻值随拉力变化的图象如图3所示,已知料斗重1×103N,没装料时Uba=0,g取10m/s2.下列说法中正确的是( )
| A. | R3阻值为40 kΩ | |
| B. | 装料时,R0的阻值逐渐变大,Uba的值逐渐变小 | |
| C. | 应变片电阻一定是用半导体材料制成的 | |
| D. | 应变片作用是把物体形变这个力学量转换为电压这个电学量 |
分析 当压敏电阻电阻值增加时,b点电势升高,故Uba的增加,将拉力的测量转化为电阻的测量.
解答 解:A、电路中,当没装料时Uba=0,此时拉力等于料斗重,为:1×103N,故应变片电阻为20KΩ,根据串并联电压关系,有:
$\frac{{R}_{1}}{{R}_{2}}=\frac{{R}_{3}}{{R}_{0}}$
解得:${R}_{3}=\frac{{R}_{0}}{{R}_{2}}{R}_{1}=\frac{20kΩ}{10KΩ}×20KΩ=40KΩ$,故A正确;
B、C、装料时,R0的阻值逐渐变大,b点电势升高,故Uba的值逐渐增加,故B错误;
D、应变片作用是把物体拉力这个力学量转换为电压这个电学量,应是由半导体材料制成的;故CD正确;
故选:ACD.
点评 本题关键理清电路结构,明确仪器的工作原理,结合串并联电路的电压和电流关系分析,不难.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
15. 如图所示,在场强大小为 E 的匀强电场中,有一个边长为L的正方形区域,正方形的一条边与电场方向平行.质量为m、电荷量绝对值为q的电子从某一条边的中点,以初速度v0射入该区域.初速度的方向垂直指向对边,但电子没有从对边飞出.下列说法正确的是( )
如图所示,在场强大小为 E 的匀强电场中,有一个边长为L的正方形区域,正方形的一条边与电场方向平行.质量为m、电荷量绝对值为q的电子从某一条边的中点,以初速度v0射入该区域.初速度的方向垂直指向对边,但电子没有从对边飞出.下列说法正确的是( )
 如图所示,在场强大小为 E 的匀强电场中,有一个边长为L的正方形区域,正方形的一条边与电场方向平行.质量为m、电荷量绝对值为q的电子从某一条边的中点,以初速度v0射入该区域.初速度的方向垂直指向对边,但电子没有从对边飞出.下列说法正确的是( )
如图所示,在场强大小为 E 的匀强电场中,有一个边长为L的正方形区域,正方形的一条边与电场方向平行.质量为m、电荷量绝对值为q的电子从某一条边的中点,以初速度v0射入该区域.初速度的方向垂直指向对边,但电子没有从对边飞出.下列说法正确的是( )| A. | 电场方向可能与初速度方向相反 | |
| B. | 电场方向可能与初速度方向垂直 | |
| C. | 电子离开该区域时,动能可能为$\frac{1}{2}$mv02 | |
| D. | 电子离开该区域时,动能可能为$\frac{1}{2}$mv02+$\frac{1}{2}$qEL |
13. 以不同的抛射角抛出三个小球A、B、C,三球在空中的运动轨迹如图所示,下列说法中正确的是( )
以不同的抛射角抛出三个小球A、B、C,三球在空中的运动轨迹如图所示,下列说法中正确的是( )
 以不同的抛射角抛出三个小球A、B、C,三球在空中的运动轨迹如图所示,下列说法中正确的是( )
以不同的抛射角抛出三个小球A、B、C,三球在空中的运动轨迹如图所示,下列说法中正确的是( )| A. | A、B、C三球在运动过程中,加速度都相同 | |
| B. | B球的射程最远,所以最迟落地 | |
| C. | A球的射高最大,所以最迟落地 | |
| D. | A、C两球的水平位移相等,所以两球的水平速度分量相等 |
17. 如图所示,圆形区域内分布着垂直纸面的匀强磁场,位于磁场边界上P点的粒子源在纸面内沿各个方向以相同的速率向磁场发射同种带电粒子,这些粒子射出边界的位置均分布在边界的某一段弧上,且这段圆弧的弧长是圆周长的$\frac{1}{3}$;若将磁感应强度的大小从B1变为B2,相应的弧长变为圆周长的$\frac{1}{6}$,则$\frac{{B}_{2}}{{B}_{1}}$等于( )
如图所示,圆形区域内分布着垂直纸面的匀强磁场,位于磁场边界上P点的粒子源在纸面内沿各个方向以相同的速率向磁场发射同种带电粒子,这些粒子射出边界的位置均分布在边界的某一段弧上,且这段圆弧的弧长是圆周长的$\frac{1}{3}$;若将磁感应强度的大小从B1变为B2,相应的弧长变为圆周长的$\frac{1}{6}$,则$\frac{{B}_{2}}{{B}_{1}}$等于( )
 如图所示,圆形区域内分布着垂直纸面的匀强磁场,位于磁场边界上P点的粒子源在纸面内沿各个方向以相同的速率向磁场发射同种带电粒子,这些粒子射出边界的位置均分布在边界的某一段弧上,且这段圆弧的弧长是圆周长的$\frac{1}{3}$;若将磁感应强度的大小从B1变为B2,相应的弧长变为圆周长的$\frac{1}{6}$,则$\frac{{B}_{2}}{{B}_{1}}$等于( )
如图所示,圆形区域内分布着垂直纸面的匀强磁场,位于磁场边界上P点的粒子源在纸面内沿各个方向以相同的速率向磁场发射同种带电粒子,这些粒子射出边界的位置均分布在边界的某一段弧上,且这段圆弧的弧长是圆周长的$\frac{1}{3}$;若将磁感应强度的大小从B1变为B2,相应的弧长变为圆周长的$\frac{1}{6}$,则$\frac{{B}_{2}}{{B}_{1}}$等于( )| A. | 2 | B. | $\sqrt{2}$ | C. | 3 | D. | $\sqrt{3}$ |
7. 有一种静电除尘的方式,如图所示,空气中的尘埃进入电离区后带上负电,然后沿平行轴线飞入金属圆筒收集区.在圆筒轴线处放有一条直线,在导线与筒壁间加上电压U,形成沿半径方向的辐向电场,假设每个尘埃的质量和带电量均相同,飞入收集区的速度相同,不计尘埃的重力,不考虑尘埃间的相互作用,则( )
有一种静电除尘的方式,如图所示,空气中的尘埃进入电离区后带上负电,然后沿平行轴线飞入金属圆筒收集区.在圆筒轴线处放有一条直线,在导线与筒壁间加上电压U,形成沿半径方向的辐向电场,假设每个尘埃的质量和带电量均相同,飞入收集区的速度相同,不计尘埃的重力,不考虑尘埃间的相互作用,则( )
 有一种静电除尘的方式,如图所示,空气中的尘埃进入电离区后带上负电,然后沿平行轴线飞入金属圆筒收集区.在圆筒轴线处放有一条直线,在导线与筒壁间加上电压U,形成沿半径方向的辐向电场,假设每个尘埃的质量和带电量均相同,飞入收集区的速度相同,不计尘埃的重力,不考虑尘埃间的相互作用,则( )
有一种静电除尘的方式,如图所示,空气中的尘埃进入电离区后带上负电,然后沿平行轴线飞入金属圆筒收集区.在圆筒轴线处放有一条直线,在导线与筒壁间加上电压U,形成沿半径方向的辐向电场,假设每个尘埃的质量和带电量均相同,飞入收集区的速度相同,不计尘埃的重力,不考虑尘埃间的相互作用,则( )| A. | 大量尘埃将聚集在导线上 | |
| B. | 尘埃在圆筒内都做类似平抛的运动 | |
| C. | 被收集尘埃的电势能减少量都相等 | |
| D. | 飞入时与圆筒轴线距离相同的尘埃到达筒壁所用的时间相同 |
11. 两小球A和B,A球系在一根长为L的轻质细绳OA上,B球系在轻质橡皮绳OB上,现将两球都拉到如图所示的水平位置上,让两绳均拉直(此时橡皮绳为原长),然后无初速释放.不计空气阻力,当两球通过最低点时,橡皮绳与细绳等长.关于小球A和B,下列说法正确的是( )
两小球A和B,A球系在一根长为L的轻质细绳OA上,B球系在轻质橡皮绳OB上,现将两球都拉到如图所示的水平位置上,让两绳均拉直(此时橡皮绳为原长),然后无初速释放.不计空气阻力,当两球通过最低点时,橡皮绳与细绳等长.关于小球A和B,下列说法正确的是( )
 两小球A和B,A球系在一根长为L的轻质细绳OA上,B球系在轻质橡皮绳OB上,现将两球都拉到如图所示的水平位置上,让两绳均拉直(此时橡皮绳为原长),然后无初速释放.不计空气阻力,当两球通过最低点时,橡皮绳与细绳等长.关于小球A和B,下列说法正确的是( )
两小球A和B,A球系在一根长为L的轻质细绳OA上,B球系在轻质橡皮绳OB上,现将两球都拉到如图所示的水平位置上,让两绳均拉直(此时橡皮绳为原长),然后无初速释放.不计空气阻力,当两球通过最低点时,橡皮绳与细绳等长.关于小球A和B,下列说法正确的是( )| A. | 通过最低点时小球A的机械能大于小球B的机械能 | |
| B. | 两小球从释放至运动到最低点的全程中机械能均守恒 | |
| C. | 两小球从释放至运动到最低点的过程中重力的冲量一定相等 | |
| D. | 小球A运动到最低点时的速率大于小球B运动到该点的速率 |
12.下列核反应方程式中,X代表α粒子(${\;}_{2}^{4}He$)的反应式是( )
| A. | ${\;}_{2}^{4}He$+${\;}_{4}^{9}Be$→${\;}_{6}^{12}C$+X | B. | ${\;}_{90}^{234}Th$→${\;}_{91}^{234}Pa$+X | ||
| C. | ${\;}_{1}^{2}H$+${\;}_{1}^{3}H$→${\;}_{0}^{1}n$+X | D. | ${\;}_{15}^{30}P$→${\;}_{14}^{30}Si$+X |

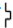 ”形状金属杆MNPQGH在辐向磁场中也以角速度ω匀速转动,如图乙所示,图丙为发电机的截面图,已知NP=GQ=R,PQ=L,MH两端接入电阻r,其余电阻不计.
”形状金属杆MNPQGH在辐向磁场中也以角速度ω匀速转动,如图乙所示,图丙为发电机的截面图,已知NP=GQ=R,PQ=L,MH两端接入电阻r,其余电阻不计.