Question

【题目】如图甲所示，平行于光滑斜面的轻弹簧劲度系数为k，一端固定在倾角为θ的斜面底端，另一端与物块A连接；B物块在斜面上紧靠着A但不粘连。两物块A. B质量分别为mA、mB，初始时物块均静止。现用平行于斜面向上的拉力F拉动物块B，使B做加速度为a的匀加速运动，两物块在开始一段时间内的vt图象如图乙所示(t1时刻A、B的图线相切)，重力加速度为g，则（）

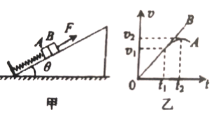
A.0-t1时间内，F一直减小

B.0-t1时间内，A、B之间的弹力一直减小

C.A. B分离时t1=

D.0-t2时间内，物块A的位移为

Answer 1

【答案】BC

【解析】

A.时间内，A、B一起运动，由牛顿第二定律可得

由于弹力逐渐减小，加速度不变，故F一直增大，A错误；

B.对B物体可得

由于F一直增大，故A、B之间弹力逐渐变小，故B正确；

C.0时刻弹簧的压缩量为，A、B分离时弹簧压缩量为，则

A、B分离时有

故A物体的位移为

由可得

故C正确；

D.时刻A物体的加速度为0，则

故A物体的位移为

故D错误；

故选BC。