��Ŀ����
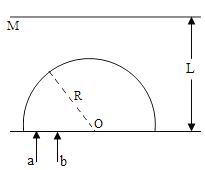
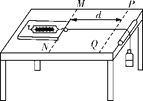
����Ŀ����ͼ��ʾ��ˮƽ���õ�Բ�̰뾶R��1 m�������ԵC��̶�һ���߶Ȳ��Ƶ�СͰ����Բ��ֱ��CD�����Ϸ�����һ��ˮƽ����AB��������CDƽ�У������Ҷ�B��Բ��Բ��O��ͬһ��ֱ���ϣ���߶Ȳ�h��1.25 m���ڻ�����˾�ֹ��������m��0.4 kg�����(����Ϊ�ʵ�)������뻬����Ķ�Ħ�������̣�0.2.����һ��СF��4 N ��ˮƽ���ҵ�������������ͬʱ��Բ�̴�ͼʾλ���Խ��ٶ��أ�2�� rad/s �ƴ���Բ��O����ֱ������ת������������һ��ʱ���������ڻ����ϼ������У���B��ˮƽ�׳���ǡ������СͰ�ڣ��������ٶ�gȡ10 m/s2����

(1)�����B����ٶȴ�С��
(2)�������õ�ʱ��t1Ӧ������Ĺ�ϵʽ��
���𰸡�(1) 2 m/s (2) ![]()
��������(1)����뿪B�����ƽ���˶�������ֱ�����У�
h��![]() gt2
gt2
����뿪B����ٶȣ�![]() ��
��
(2)�������ʱ�ļ��ٶ�����ţ�ٵڶ����ɣ�F����mg��ma1��
�ã�a1��8 m/s2,
��ȥ�������ļ��ٶȣ�a2����g��2 m/s2��
��ת��һȦ��ʱ�䣺![]() ��
��
����ڻ������ȼ��ٺ���٣�v��a1t1��a2t2
��黬��ʱ�䡢�ڿ��е��˶�ʱ����Բ�����ڹ�ϵ��
t1��t2��t��nT
��������ʽ������![]() ��
��
������ǣ�(1) 2 m/s (2) ![]()

 �»����ܶ�Ա��ϵ�д�
�»����ܶ�Ա��ϵ�д� ����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�
����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�