题目内容
质量为M的拖拉机拉着耙来耙地,由静止开始做匀加速直线运动,在时间t内前进的距离为s.耙地时,拖拉机受到的牵引力恒为F,受到地面的阻力为自重的k倍,把所受阻力恒定,连接杆质量不计且与水平面的夹角θ保持不变.则可求出的物理量是( )
A.t秒末拖拉机对耙的做功的功率
B.t秒末耙的动能
C.拖拉机的加速度
D.连接杆拉力的大小
【答案】分析:拖拉机对耙的牵引力为F,拖拉机在t秒内前进的距离为s,根据功率的公式可求出t秒末拖拉机对耙的做功的功率.耙的质量未知,不能求出耙的动能.根据运动学公式求出拖拉机的加速度.根据牛顿第二定律求出连接杆拉力的大小.
解答:解:
A、设t秒末耙的速度大小为v,则由s=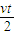 得,v=
得,v=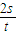 ,则t秒末拖拉机对耙的做功的功率为P=Fvcosθ=F
,则t秒末拖拉机对耙的做功的功率为P=Fvcosθ=F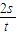 cosθ=
cosθ=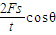 ,F、s、t、θ都已知,所以可以求出t秒末拖拉机对耙的做功的功率.故A正确.
,F、s、t、θ都已知,所以可以求出t秒末拖拉机对耙的做功的功率.故A正确.
B、由于耙的质量未知,无法求出t秒末耙的动能.故B错误.
C、根据运动学公式得:s=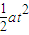 ,得a=
,得a=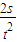 ,t、s均已知,所以拖拉机的加速度可以求出.故C正确.
,t、s均已知,所以拖拉机的加速度可以求出.故C正确.
D、设连接杆的拉力大小为T.根据牛顿第二定律得:F-Tcosθ-kMg=Ma,F、θ、M、a都已知或求出,所以可以求出连接杆的拉力T的大小.故D正确.
故选ACD
点评:本题考查运用功率公式、运动学公式、牛顿第二定律研究匀变速直线运动中拉力的功率、物体的动能和加速度等的能力.
解答:解:
A、设t秒末耙的速度大小为v,则由s=
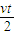 得,v=
得,v=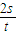 ,则t秒末拖拉机对耙的做功的功率为P=Fvcosθ=F
,则t秒末拖拉机对耙的做功的功率为P=Fvcosθ=F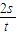 cosθ=
cosθ=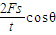 ,F、s、t、θ都已知,所以可以求出t秒末拖拉机对耙的做功的功率.故A正确.
,F、s、t、θ都已知,所以可以求出t秒末拖拉机对耙的做功的功率.故A正确.B、由于耙的质量未知,无法求出t秒末耙的动能.故B错误.
C、根据运动学公式得:s=
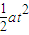 ,得a=
,得a=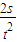 ,t、s均已知,所以拖拉机的加速度可以求出.故C正确.
,t、s均已知,所以拖拉机的加速度可以求出.故C正确.D、设连接杆的拉力大小为T.根据牛顿第二定律得:F-Tcosθ-kMg=Ma,F、θ、M、a都已知或求出,所以可以求出连接杆的拉力T的大小.故D正确.
故选ACD
点评:本题考查运用功率公式、运动学公式、牛顿第二定律研究匀变速直线运动中拉力的功率、物体的动能和加速度等的能力.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案
相关题目
 (2010?四川)质量为M的拖拉机拉着耙来耙地,由静止开始做匀加速直线运动,在时间t内前进的距离为s.耙地时,拖拉机受到的牵引力恒为F,受到地面的阻力为自重的k倍,耙所受阻力恒定,连接杆质量不计且与水平面的夹角θ保持不变.求:
(2010?四川)质量为M的拖拉机拉着耙来耙地,由静止开始做匀加速直线运动,在时间t内前进的距离为s.耙地时,拖拉机受到的牵引力恒为F,受到地面的阻力为自重的k倍,耙所受阻力恒定,连接杆质量不计且与水平面的夹角θ保持不变.求: 质量为M的拖拉机拉着耙来耙地,由静止开始做匀加速直线运动,在时间t内前进的距离为s.耙地时,拖拉机受到的牵引力恒为F,受到地面的阻力为自重的k倍,把所受阻力恒定,连接杆质量不计且与水平面的夹角θ保持不变.求:
质量为M的拖拉机拉着耙来耙地,由静止开始做匀加速直线运动,在时间t内前进的距离为s.耙地时,拖拉机受到的牵引力恒为F,受到地面的阻力为自重的k倍,把所受阻力恒定,连接杆质量不计且与水平面的夹角θ保持不变.求:
 (1)拖拉机的加速度大小。
(1)拖拉机的加速度大小。