题目内容
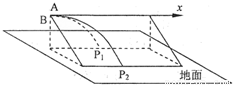
如图所示,A、B两质点从同一位置以相同的水平初速v抛出,A在竖直面内运动,落地点为P1,B沿光滑斜面运动,落地点为P2,不计阻力,比较P1、P2在水平x轴方向上距抛出点的远近关系及落地时速度的大小关系,正确的是( )①P2较远
②P1、P2一样远
③A落地时速率大
④A、B落地时速率一样大.
A.①③
B.②③
C.①④
D.②④
【答案】分析:A质点做平抛运动,
B质点视为在光滑斜面上的类平抛运动,其加速度为gsinθ,根据平抛规律与A运动对比求解时间和位移.
根据动能定理研究比较A、B落地时的速度大小.
解答:解:A质点做平抛运动,根据平抛规律得:
A运动时间:t=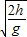 ,
,
B质点视为在光滑斜面上的类平抛运动,其加速度为gsinθ,
B运动时间:t′=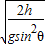 .
.
A、B沿x轴方向都做水平速度相等的匀速直线运动,由于运动时间不等,所以沿x轴方向的位移大小不同,P2较远,故①正确,②错误.
根据动能定理得A、B运动过程中:mgh= mv2-
mv2-
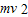
解得:v=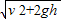 ,故A、B落地时速率一样大,即③错误,④正确.
,故A、B落地时速率一样大,即③错误,④正确.
故①④正确;
故选C.
点评:本题关键是先确定B参与沿与水平方向和沿斜面方向的运动,然后根据合运动与分运动的等效性,由平行四边形定则求解.
B质点视为在光滑斜面上的类平抛运动,其加速度为gsinθ,根据平抛规律与A运动对比求解时间和位移.
根据动能定理研究比较A、B落地时的速度大小.
解答:解:A质点做平抛运动,根据平抛规律得:
A运动时间:t=
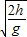 ,
,B质点视为在光滑斜面上的类平抛运动,其加速度为gsinθ,
B运动时间:t′=
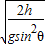 .
.A、B沿x轴方向都做水平速度相等的匀速直线运动,由于运动时间不等,所以沿x轴方向的位移大小不同,P2较远,故①正确,②错误.
根据动能定理得A、B运动过程中:mgh=
 mv2-
mv2-
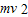
解得:v=
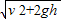 ,故A、B落地时速率一样大,即③错误,④正确.
,故A、B落地时速率一样大,即③错误,④正确.故①④正确;
故选C.
点评:本题关键是先确定B参与沿与水平方向和沿斜面方向的运动,然后根据合运动与分运动的等效性,由平行四边形定则求解.

练习册系列答案
相关题目
 如图所示,A、B两小球由绕过轻质定滑轮的细线相连,A放在固定的光滑斜面上,B、C两小球在竖直方向上通过劲度系数为k的轻质弹簧相连,C球放在水平地面上.现用手控制住A,并使细线刚刚拉直但无拉力作用,并保证滑轮左侧细线竖直、右侧细线与斜面平行.已知A的质量为3m,B、C的质量均为m,重力加速度为g,细线与滑轮之间的摩擦不计,开始时整个系统处于静止状态.释放A后,A沿斜面下滑至速度最大时C恰好离开地面.则下列说法正确的是( )
如图所示,A、B两小球由绕过轻质定滑轮的细线相连,A放在固定的光滑斜面上,B、C两小球在竖直方向上通过劲度系数为k的轻质弹簧相连,C球放在水平地面上.现用手控制住A,并使细线刚刚拉直但无拉力作用,并保证滑轮左侧细线竖直、右侧细线与斜面平行.已知A的质量为3m,B、C的质量均为m,重力加速度为g,细线与滑轮之间的摩擦不计,开始时整个系统处于静止状态.释放A后,A沿斜面下滑至速度最大时C恰好离开地面.则下列说法正确的是( )| A、斜面倾角α=37° | ||||
B、A获得最大速度为g
| ||||
| C、C刚离开地面时,B的加速度最大 | ||||
| D、从释放A到C刚离开地面的过程中,A、B两小球组成的系统机械能守恒 |
 (2008?苏州模拟)如图所示,A、B两物体与一轻质弹簧相连,静止在地面上,有一小物体C从距A物体h高度处由静止释放,当下落至与A相碰后立即粘在一起向下运动,以后不再分开,当A与C运动到最高点时,物体B对地面刚好无压力、设A、B、C三物体的质量均为m,弹簧的劲度k,不计空气阻力且弹簧始终处于弹性限度内.若弹簧的弹性势能由弹簧劲度系数和形变量决定,求C物体下落时的高度h.
(2008?苏州模拟)如图所示,A、B两物体与一轻质弹簧相连,静止在地面上,有一小物体C从距A物体h高度处由静止释放,当下落至与A相碰后立即粘在一起向下运动,以后不再分开,当A与C运动到最高点时,物体B对地面刚好无压力、设A、B、C三物体的质量均为m,弹簧的劲度k,不计空气阻力且弹簧始终处于弹性限度内.若弹簧的弹性势能由弹簧劲度系数和形变量决定,求C物体下落时的高度h. 如图所示,A、B两物块始终静止在水平地面上,有一轻质弹簧一端连接在竖直墙上P点,另一端与A相连接,下列说法正确的是( )
如图所示,A、B两物块始终静止在水平地面上,有一轻质弹簧一端连接在竖直墙上P点,另一端与A相连接,下列说法正确的是( ) 如图所示,A、B两小球由绕过轻质定滑轮的细线相连,A放在固定的光滑斜面上,B、C两小球在竖直方向上通过劲度系数为k的轻质弹簧相连,C球放在水平地面上.现用手控制住A,并使细线刚刚拉直但无拉力作用,并保证滑轮左侧细线竖直、右侧细线与斜面平行.已知A的质量为4m,B、C的质量均为m,重力加速度为g,细线与滑轮之间的摩擦不计,开始时整个系统处于静止状态.释放A后,A沿斜面下滑至速度最大时C恰好离开地面.下列说法正确的是( )
如图所示,A、B两小球由绕过轻质定滑轮的细线相连,A放在固定的光滑斜面上,B、C两小球在竖直方向上通过劲度系数为k的轻质弹簧相连,C球放在水平地面上.现用手控制住A,并使细线刚刚拉直但无拉力作用,并保证滑轮左侧细线竖直、右侧细线与斜面平行.已知A的质量为4m,B、C的质量均为m,重力加速度为g,细线与滑轮之间的摩擦不计,开始时整个系统处于静止状态.释放A后,A沿斜面下滑至速度最大时C恰好离开地面.下列说法正确的是( ) (2011?辽宁二模)(1)下列说法正确的是
(2011?辽宁二模)(1)下列说法正确的是