题目内容
如图所示，“神舟”飞船升空后，进入近地点为B，远地点为A的椭圆轨道I上飞行．飞行数圈后变轨．在过远地点A的圆轨道Ⅱ上做匀速圆周运动．飞船由椭圆轨道运行变轨到圆形轨道运行后（ ）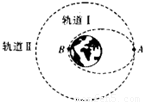
A．周期变短．机械能增加
B．周期变短，机械能减小
C．周期变长，机械能增加
D．周期变长，机械能减小
【答案】分析：根据开普勒第三定律求出周期的变化情况．
飞船机械能是否变化要看是否有外力对飞船做功，当万有引力刚好提供飞船所需向心力时 飞船正好可以做匀速圆周运动，若是供大于需 则飞船做逐渐靠近圆心的运动，若是供小于需 则飞船做逐渐远离圆心的运动．
解答：解：根据开普勒第三定律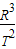
=k，得：
飞船由椭圆轨道运行变轨到圆形轨道运行后R将变大，所以周期也变长．
在椭圆轨道远地点实施变轨成圆轨道是做逐渐远离圆心的运动，要实现这个运动必须万有引力小于飞船所需向心力，所以应给飞船加速，增加所需的向心力．
因为飞船在远地点P点火加速，外力对飞船做功，故飞船在此过程中机械能增加．
故选C．
点评：卫星变轨问题，要抓住确定轨道上运行机械能守恒，在不同轨道上的卫星其机械能不同，轨道越大机械能越大．
飞船机械能是否变化要看是否有外力对飞船做功，当万有引力刚好提供飞船所需向心力时 飞船正好可以做匀速圆周运动，若是供大于需 则飞船做逐渐靠近圆心的运动，若是供小于需 则飞船做逐渐远离圆心的运动．
解答：解：根据开普勒第三定律
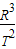=k，得：飞船由椭圆轨道运行变轨到圆形轨道运行后R将变大，所以周期也变长．
在椭圆轨道远地点实施变轨成圆轨道是做逐渐远离圆心的运动，要实现这个运动必须万有引力小于飞船所需向心力，所以应给飞船加速，增加所需的向心力．
因为飞船在远地点P点火加速，外力对飞船做功，故飞船在此过程中机械能增加．
故选C．
点评：卫星变轨问题，要抓住确定轨道上运行机械能守恒，在不同轨道上的卫星其机械能不同，轨道越大机械能越大．
练习册系列答案
相关题目
2011年11月3日凌晨1时43分，“神舟八号”与“天宮一号”成功对接．从对接机构接触开始，经过捕获、缓冲、拉近、锁紧4个步骤，“神舟八号”飞船与“天宫一号”目标飞器3日凌晨实现刚性连接，形成组合体，中国载人航天首次空间交会对接试验获得成功．假设对接前它们在各自轨道上绕地球做匀速圆周运动，如图所示，则下列说法中正确的是（ ）
