题目内容
如图所示，光滑绝缘半球槽的半径为R，处在水平向右的匀强电场中，一质量为m的带正电的小球从槽的右端A点无初速沿轨道滑下，滑到最低位置B点时，对轨道的压力为2mg.求：
（1）小球所受的电场力大小；
（2）带电小球速度最大时的位置与圆心O的连线跟竖直方向的夹角（用反三角函数表示）.
(1)
mg (2)arctan
解析：（1）设小球在最低点的速度为v，轨道对小球的支持力F=2mg，
则：F-mg=mg=m
，所以：v=
.
设小球所受的电场力大小为F1，对小球从A点滑到最低位置B点的过程用动能定理得：mgR-F1R=
mv2，F1=
mg.
（2）设小球滑到D点时的速度最大，则在D点，重力沿圆弧切线方向上的分力G1与电场力在圆弧切线方向上的分力F1′平衡，如图所示，即：
mgsinθ=F1cosθ,tanθ=
θ，=arctan
.
练习册系列答案
相关题目
如图所示，在竖直放置的光滑半圆弧绝缘细管的圆心O处固定一点电荷，将质量为m，带电量为+q的小球从圆弧管的水平直径端点A由静止释放，小球沿细管滑到最低点B时，对管壁恰好无压力．求：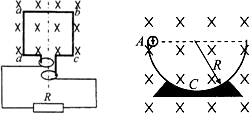
（1）如图所示，线圈abcd的面积是0.05m2，共100匝；线圈总电阻r=1Ω，外接电阻R=9Ω，匀强磁场的磁感应强度B=
一端弯曲的光滑绝缘轨道ABD固定在竖直平面上，如图所示，AB段水平、BD段是半径为R的半圆弧，有电荷量为Q的正点电荷固定在圆心O处．一质量为m、电荷量为q的带正电小环，在水平恒力F0作用下从C点由静止开始运动，到B点时撤去外力，小环继续运动，发现刚好能到达绝缘轨道上与圆心等高的M点，已知CB间距为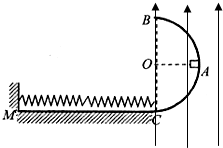
如图所示，光滑半圆弧绝缘轨道半径为R，OA为水平半径，BC为竖直直径．一质量为m且始终带+q电量的小物块自A处以某一竖直向下的初速度滑下，进入与C点相切的粗糙水平绝缘滑道CM上，在水平滑道上有一轻弹簧，其一端固定在竖直墙上，另一端恰位于滑道的末端C点，此时弹簧处于自然状态．物块运动过程中弹簧最大弹性势能为EP，物块被弹簧反弹后恰能通过B点．己知物块与水平滑道间的动摩擦因数为μ，直径BC右侧所处的空间（包括BC边界）有竖直向上的匀强电场，且电场力为重力的一半．求：