题目内容
不可回收的航天器在使用后,将成为太空垃圾.如图是漂浮在地球附近的太空垃圾示意图,对此有如下说法,正确的是( )
A.离地越低的太空垃圾运行周期越小
B.离地越高的太空垃圾运行角速度越小
C.由公式
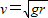 得,离地越高的太空垃圾运行速率越大
得,离地越高的太空垃圾运行速率越大D.太空垃圾一定能跟同一轨道上同向飞行的航天器相撞
【答案】分析:太空垃圾绕地球做匀速圆周运动,地球的万有引力提供向心力,由牛顿第二定律列方程,求出线速度、角速度、周期的表达式,然后答题.
解答:解:设地球质量为M,垃圾质量为m,垃圾的轨道半径为r;
A、由牛顿第二定律可得:G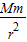 =m
=m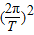 r,垃圾的运行周期:T=2π
r,垃圾的运行周期:T=2π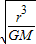 ,
,
∵2、π、G、M是常数,∴r越小,即离地越低的太空垃圾运行周期越小,故A正确;
B、由牛顿第二定律可得:G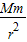 =mω2r,垃圾运行的角速度ω=
=mω2r,垃圾运行的角速度ω=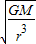 ,
,
∵G、M是常数,∴轨道半径越大,即离地越高的垃圾的角速度越小,故B正确;
C、由牛顿第二定律可得:G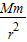 =m
=m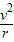 ,垃圾运行的线速度v=
,垃圾运行的线速度v=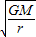 ,
,
∵G、M是常数,∴轨道半径越大,即离地越高的垃圾线速度越小,故C错误;
D、由线速度公式v=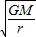 可知,在同一轨道上的航天器与太空垃圾线速度相同,
可知,在同一轨道上的航天器与太空垃圾线速度相同,
如果它们绕地球飞行的运转方向相同,它们不会碰撞,故D错误;
故选AB.
点评:本题考查了太空垃圾的线速度、周期、角速度大小问题,难度不大,知道地球引力提供向心力、熟练应用牛顿定律列方程即可正确解题.
解答:解:设地球质量为M,垃圾质量为m,垃圾的轨道半径为r;
A、由牛顿第二定律可得:G
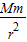 =m
=m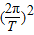 r,垃圾的运行周期:T=2π
r,垃圾的运行周期:T=2π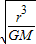 ,
,∵2、π、G、M是常数,∴r越小,即离地越低的太空垃圾运行周期越小,故A正确;
B、由牛顿第二定律可得:G
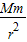 =mω2r,垃圾运行的角速度ω=
=mω2r,垃圾运行的角速度ω=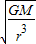 ,
,∵G、M是常数,∴轨道半径越大,即离地越高的垃圾的角速度越小,故B正确;
C、由牛顿第二定律可得:G
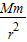 =m
=m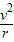 ,垃圾运行的线速度v=
,垃圾运行的线速度v=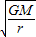 ,
,∵G、M是常数,∴轨道半径越大,即离地越高的垃圾线速度越小,故C错误;
D、由线速度公式v=
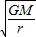 可知,在同一轨道上的航天器与太空垃圾线速度相同,
可知,在同一轨道上的航天器与太空垃圾线速度相同,如果它们绕地球飞行的运转方向相同,它们不会碰撞,故D错误;
故选AB.
点评:本题考查了太空垃圾的线速度、周期、角速度大小问题,难度不大,知道地球引力提供向心力、熟练应用牛顿定律列方程即可正确解题.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
不可回收的航天器在使用后,将成为太空垃圾。如图所示是漂浮在地球附近的太空垃圾示意图,对此有如下说法,正确的是( )
| A.离地越低的太空垃圾运行周期越小 |
| B.离地越高的太空垃圾运行角速度越小 |
C.由公式v= 得,离地越高的太空垃圾运行速率越大 得,离地越高的太空垃圾运行速率越大 |
| D.太空垃圾一定能跟同一轨道上同向飞行的航天器相撞 |
不可回收的航天器在使用后,将成为太空垃圾。如图所示是漂浮在地球附近的太空垃圾示意图,下列说法中正确的是( )
| A.离地越高的太空垃圾运行速率越大 |
| B.离地越高的太空垃圾运行角速度越小 |
| C.离地越高的太空垃圾运行周期越大 |
| D.太空垃圾一定能跟同一轨道上同向飞行的航天器相撞 |
 (2012?惠州二模)不可回收的航天器在使用后,将成为太空垃圾.如图是漂浮在地球附近的太空垃圾示意图,对此有如下说法,正确的是( )
(2012?惠州二模)不可回收的航天器在使用后,将成为太空垃圾.如图是漂浮在地球附近的太空垃圾示意图,对此有如下说法,正确的是( )

 得,离地越高的太空垃圾运行速率越大
得,离地越高的太空垃圾运行速率越大