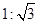题目内容
如图所示是倾角为45°的斜坡，在斜坡底端P点正上方某一位置Q处以速度v水平向左抛出一个小球A，小球恰好能垂直落在斜坡上，运动时间为t1．小球B从同一点Q处自由下落，下落至P点的时间为t2．不计空气阻力，则t1：t2=（ ）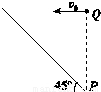
A．1：2
B．1：
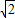
C．1：3
D．1：
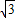
【答案】分析：小球做平抛运动时，根据分位移公式求出竖直分位移和水平分位移之比，然后根据几何关系求解出的自由落体运动的位移并求出时间．
解答：解：小球A恰好能垂直落在斜坡上，如图
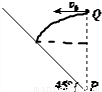
由几何关系可知，小球竖直方向的速度增量
vy=gt1=v ①
水平位移S=vt1 ②
竖直位移hQ=
g
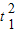③
由①②③得到：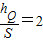
由几何关系可知小球B作自由下落的高度为：
hQ+S═
g
④
联立以上各式解得：
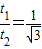
故选D．
点评：本题关键是明确小球Q的运动是平抛运动，然后根据平抛运动的分位移和分速度公式联立求解出运动时间，再根据几何关系得到自由落体的位移，从而进一步求得时间，最后得到比值．
解答：解：小球A恰好能垂直落在斜坡上，如图
由几何关系可知，小球竖直方向的速度增量
vy=gt1=v ①
水平位移S=vt1 ②
竖直位移hQ=
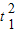g ③由①②③得到：
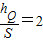
由几何关系可知小球B作自由下落的高度为：
hQ+S═
g ④联立以上各式解得：
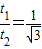
故选D．
点评：本题关键是明确小球Q的运动是平抛运动，然后根据平抛运动的分位移和分速度公式联立求解出运动时间，再根据几何关系得到自由落体的位移，从而进一步求得时间，最后得到比值．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
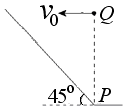
如图所示是倾角为45°的斜坡，在斜坡底端P点正上方某一位置Q处以速度v0水平向左抛出一个小球A，小球恰好能垂直落在斜坡上，运动时间为t1．小球B从同一点Q处自由下落，下落至P点的时间为t2．不计空气阻力，则t1：t2=（ ）
如图所示是倾角为45°的斜坡，在斜坡底端P点正上方某一位置Q处以速度v0水平向左抛出一个小球A，小球恰好能垂直落在斜坡上，运动时间为t1．小球B从同一点Q处自由下落，下落至P点的时间为t2．不计空气阻力，请计算t1：t2的值．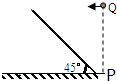
如图所示是倾角为45°的斜坡，在斜坡底端P点正上方某一位置Q处以某一初速度水平向左抛出一个小球A，小球恰好能垂直落在斜坡上，运动时间为t1；小球B从Q处自由下落，下落至P点的时间为t2．不计空气阻力，t1：t2等于（ ）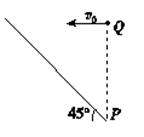
水平向左抛出一个小球A，小球恰好能垂直落在斜坡上，运动时间为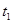
.小球B从同一点Q处自由下落，下落至P点的时间为
.不计空气阻力，则
（ ）
C．1∶3 D．