题目内容
 在竖直平面内有一个半径为R的光滑圆环轨道,一个质量为m的小球穿在圆环轨道上做圆周运动,如图所示,到达最高点C时的速率是vC=
在竖直平面内有一个半径为R的光滑圆环轨道,一个质量为m的小球穿在圆环轨道上做圆周运动,如图所示,到达最高点C时的速率是vC=
|
分析:因为圆环轨道是光滑的,只有重力做功,所以机械能守恒,可以求得在最低点时的最大速度;
对物体受力分析,根据圆周运动的向心力公式可以求得对轨道的作用力,由周期公式可以知道物体运动的周期.
对物体受力分析,根据圆周运动的向心力公式可以求得对轨道的作用力,由周期公式可以知道物体运动的周期.
解答:解:A、速度最大的点应该是最低点时,根据动能定理:
mV2-
mVc2=2mgR,解得V=
=
Vc,所以A正确.
B、在C点有:mg-T=m
,得T=
mg,所以B错误.
C、整个过程中机械能守恒,在任一直径两端点上的点,它们的高度之和都是2R,即它们的重力势能的和相等,由于总的机械能守恒,所以它们的动能之和也相等,所以C正确.
D、由T=
,当速度最小时,代入计算可得T=π
,之后小球的速度在变大,所以T要减小,所以T<π
,所以D正确.
故选ACD.
| 1 |
| 2 |
| 1 |
| 2 |
|
| 6 |
B、在C点有:mg-T=m
| ||
| R |
| 1 |
| 5 |
C、整个过程中机械能守恒,在任一直径两端点上的点,它们的高度之和都是2R,即它们的重力势能的和相等,由于总的机械能守恒,所以它们的动能之和也相等,所以C正确.
D、由T=
| 2πR |
| V |
|
|
故选ACD.
点评:小球穿在圆环轨道上做圆周运动,属于杆的模型,在最高点时速度最小,向心力最小,最低点时速度最大,向心力最大,由机械能守恒可以求它们之间的关系.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 在xoy竖直平面内,仅在第一、四象限分布着竖直向上的匀强电场E,第一象限还存在着垂直纸面向里的匀强磁场B,方向如图所示.在y轴负向A点处有一质量为1.0×10-6 kg,电量为q=1.0×10-6 c的带正电微粒以初速度v0=8m/s,垂直y轴射入第四象限内.其中电场强度E=20N/c,OA的长为d=1.8m,g取10m/s2.
在xoy竖直平面内,仅在第一、四象限分布着竖直向上的匀强电场E,第一象限还存在着垂直纸面向里的匀强磁场B,方向如图所示.在y轴负向A点处有一质量为1.0×10-6 kg,电量为q=1.0×10-6 c的带正电微粒以初速度v0=8m/s,垂直y轴射入第四象限内.其中电场强度E=20N/c,OA的长为d=1.8m,g取10m/s2.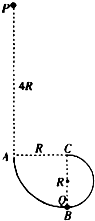 如图所示,质量为m的小球P自距离A点4R高处下落,然后沿A点切线方向进入竖直平面内的光滑轨道ABC.AB是半径为R的
如图所示,质量为m的小球P自距离A点4R高处下落,然后沿A点切线方向进入竖直平面内的光滑轨道ABC.AB是半径为R的 ,电量为
,电量为 的带正电微粒以初速度
的带正电微粒以初速度 ,垂直y轴射入第四象限内。其中电场强度
,垂直y轴射入第四象限内。其中电场强度 ,OA的长为
,OA的长为 ,g取
,g取 。
。
 ;
;