题目内容
如图所示,长度为三的轻绳一端固定在天花板上,另一端连一个质量为m的小球,在距悬点高度差为 的光滑水平面内做匀速圆周运动,试求下列情况下绳子拉力的大小
的光滑水平面内做匀速圆周运动,试求下列情况下绳子拉力的大小(1)小球速度为

(2)小球速度为
 .
.
【答案】分析:小球在水平面内绕O点作匀速圆周运动,由绳子拉力的水平分力提供向心力,由平行四边形定则,作出重力与拉力的合力,根据牛顿第二定律求出绳子的拉力.
解答:解:(1)当小球的速度为为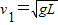 时,设绳子拉力大小为T1,水平面的支持力为N1,则根据牛顿第二定律得
时,设绳子拉力大小为T1,水平面的支持力为N1,则根据牛顿第二定律得
T1sinα+N1=mg ①
T1cosα=m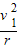 ②
②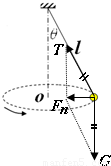
又r=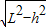 =
=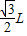 ,cosα=
,cosα=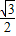
代入解得,T1= mg,N1=
mg,N1= mg
mg
(2)由①②得,当N1=0时,v1=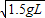 ,故当小球速度为
,故当小球速度为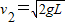 时,小球离开水平面做匀速圆周运动,此时由重力与绳子拉力的合力提供向心力,受力如图,由平行四边形定则得:
时,小球离开水平面做匀速圆周运动,此时由重力与绳子拉力的合力提供向心力,受力如图,由平行四边形定则得:
mg=T2cosθ
T2sinθ=m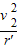
又r′=Lsinθ
联立以上三式解得,T2=(1+2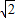 )mg
)mg
答:(1)小球速度为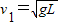 时绳子的拉力大小为
时绳子的拉力大小为 mg;
mg;
(2)小球速度为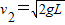 时绳子的拉力大小为(1+2
时绳子的拉力大小为(1+2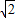 )mg.
)mg.
点评:本题关键要分析得出速度为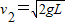 时小球已离开水平面,挖掘隐含的临界状态.
时小球已离开水平面,挖掘隐含的临界状态.
解答:解:(1)当小球的速度为为
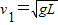 时,设绳子拉力大小为T1,水平面的支持力为N1,则根据牛顿第二定律得
时,设绳子拉力大小为T1,水平面的支持力为N1,则根据牛顿第二定律得T1sinα+N1=mg ①
T1cosα=m
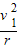 ②
②
又r=
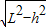 =
=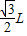 ,cosα=
,cosα=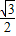
代入解得,T1=
 mg,N1=
mg,N1= mg
mg(2)由①②得,当N1=0时,v1=
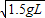 ,故当小球速度为
,故当小球速度为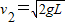 时,小球离开水平面做匀速圆周运动,此时由重力与绳子拉力的合力提供向心力,受力如图,由平行四边形定则得:
时,小球离开水平面做匀速圆周运动,此时由重力与绳子拉力的合力提供向心力,受力如图,由平行四边形定则得:mg=T2cosθ
T2sinθ=m
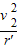
又r′=Lsinθ
联立以上三式解得,T2=(1+2
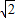 )mg
)mg答:(1)小球速度为
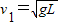 时绳子的拉力大小为
时绳子的拉力大小为 mg;
mg;(2)小球速度为
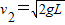 时绳子的拉力大小为(1+2
时绳子的拉力大小为(1+2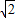 )mg.
)mg.点评:本题关键要分析得出速度为
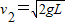 时小球已离开水平面,挖掘隐含的临界状态.
时小球已离开水平面,挖掘隐含的临界状态. 
练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 如图所示,长度为三的轻绳一端固定在天花板上,另一端连一个质量为m的小球,在距悬点高度差为
如图所示,长度为三的轻绳一端固定在天花板上,另一端连一个质量为m的小球,在距悬点高度差为 、
、 ,则关于
,则关于 、
、 两力的合力大小、方向的说法正确的是
两力的合力大小、方向的说法正确的是
 、
、 大小未知,不能确定
大小未知,不能确定
