题目内容
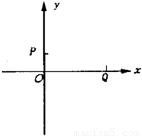如图所示，在第一象限有一匀强电场，场强大小为E，方向与y轴平行；在x轴下方有一匀强磁场，磁场方向与纸面垂直．一质量为m、电荷量为-q（q＞0）的粒子以平行于x轴的速度从y轴上的P点处射入电场，在x轴上的Q点处进入磁场，并从坐标原点O离开磁场．粒子在磁场中的运动轨迹与y轴交于M点．已知OP=l，OQ=2
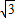l．不计重力．求：（1）M点与坐标原点O间的距离；
（2）粒子从P点运动到M点所用的时间．
【答案】分析：分析粒子在电场和磁场中的运动性质，在电场中做类平抛运动，在磁场中做匀速圆周运动，由牛顿第二定律和平抛运动的知识求MO的长度，进而可以求运动的时间．
解答：解：（1）带电粒子在电场中做类平抛运动，在y轴负方向上做初速度为零的匀加速运动，设加速度的大小为a；在x轴正方向上做匀速直线运动，设速度为v；粒子从P点运动到Q点所用的时间为t1，进入磁场时速度方向与x轴正方向的夹角为θ，则
由牛顿第二定律得：qE=ma①
在电场中运动的时间为：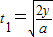
②
水平初速度：
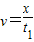③
其中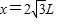
2，y=L，又tanθ=
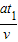④
联立②③④得θ=30°⑤
由几何关系知MQ为直径，R=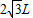
⑥
MO=
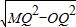=6L⑦
（2）设粒子在磁场中运动的速度为v，从Q到M点运动的时间为t2，则有
v=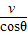
⑧
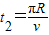⑨
从P点到M点所用的时间t=t1+t2⑩
联立①②③⑤⑥⑧⑨⑩并代入数据得
t=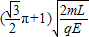
（1）M点与坐标原点O间的距离为6L；
（2）粒子从P点运动到M点所用的时间为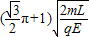
．
点评：解决此类题目的关键是知道粒子在各个阶段的运动性质，再分别应用不同的知识去求解，可以先画出草图再分析．
解答：解：（1）带电粒子在电场中做类平抛运动，在y轴负方向上做初速度为零的匀加速运动，设加速度的大小为a；在x轴正方向上做匀速直线运动，设速度为v；粒子从P点运动到Q点所用的时间为t1，进入磁场时速度方向与x轴正方向的夹角为θ，则
由牛顿第二定律得：qE=ma①
在电场中运动的时间为：
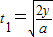②水平初速度：
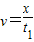③其中
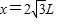2，y=L，又tanθ=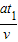④联立②③④得θ=30°⑤
由几何关系知MQ为直径，R=
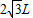⑥MO=
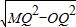=6L⑦（2）设粒子在磁场中运动的速度为v，从Q到M点运动的时间为t2，则有
v=
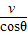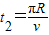⑧⑨从P点到M点所用的时间t=t1+t2⑩
联立①②③⑤⑥⑧⑨⑩并代入数据得
t=
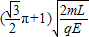
（1）M点与坐标原点O间的距离为6L；
（2）粒子从P点运动到M点所用的时间为
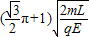．点评：解决此类题目的关键是知道粒子在各个阶段的运动性质，再分别应用不同的知识去求解，可以先画出草图再分析．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
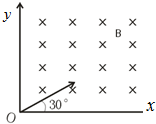（2011?南县模拟）如图所示，在第一象限内有垂直纸面向里的匀强磁场，一对正、负电子分别以相同速度沿与x轴成30°角从原点垂直射入磁场，则正、负电子在磁场中运动时间之比为（ ）
如图所示，在第一象限内有垂直纸面向里的匀强磁场，一对正、负电子分别以相同速度沿与x轴成60°角从原点射入磁场，则正、负电子在磁场中运动时间之比为（ ）
如图所示，在第一象限内有垂直纸面向里的匀强磁场，一对质量和电荷量均相等的正、负离子（不计重力）分别以相同速度沿与x轴成30°角从原点射入磁场，则正、负离子在磁场中（ ）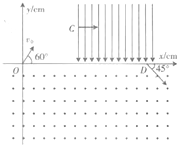
（2013?山西模拟）如图所示，在第一象限0＜x＜6cm的范围内，有一方向垂直于纸面向外、磁感应强度大小为B1=0.8T的圆形匀强磁场区域（图中未画出），在x＞6cm的范围内有沿y轴负方向的匀强电场；第三、四象限内有垂直纸面向外的匀强磁场，磁感应强度B2的大小未知．一个质量m=8.0×10-l2kg、电荷量q=2.0×l0-6C的带正电的粒子，以v0=4.0×l03m/s的速度从坐标原点O沿与x轴正方向成60°角射出，经圆形匀强磁场区域后平行x轴方向到达C（6cm，4cm ）点，之后从C点垂直电场方向射入匀强电场中，并从D点沿与x轴正方向成45°角进入匀强磁场B2中，最后恰好能返回到O点．不计带电粒子的重力，求：
如图所示，在第一象限存在垂直纸面向里大小为B的无限大的匀强磁场，一个质量为m，电量为q带正电的粒子从坐标原点O处以v进人磁场，粒子进入磁场时的速度方向垂直于磁场，且与x轴正方向成30．角，不计重力，则粒子在磁场中运动的时间和半径为（ ）A、t=
| ||
B、t=
| ||
C、R=
| ||
D、R=
|