题目内容
19. 在一个匀强电场(图中未画出)的平面内有一个四边形ABCD,E为AD的中点,F为BC的中点,一个带正电的粒子从A移动到B点,电场力做功0.8×10-8J,将该粒子从D移到C点,电场力做功为2.4×10-8 J,将粒子从E点移到F点,则下列分析正确的是( )
在一个匀强电场(图中未画出)的平面内有一个四边形ABCD,E为AD的中点,F为BC的中点,一个带正电的粒子从A移动到B点,电场力做功0.8×10-8J,将该粒子从D移到C点,电场力做功为2.4×10-8 J,将粒子从E点移到F点,则下列分析正确的是( )| A. | 若粒子的电荷量为2.4×10-8C,则D、C之间的电势差为1V | |
| B. | 若A、B之间的距离为1cm,粒子的电荷量为0.8×10-8C,该电场的场强一定是E=100 V/m | |
| C. | 若将该粒子从E点移动到F点,电场力做功WEF有可能大于1.6×10-8J | |
| D. | 若将该粒子从E点移动到F点,电场力做功为1.6×10-8 J |
分析 E为AD的中点,F为BC的中点,根据公式U=Ed可知,匀强电场中沿着电场线方向,两点间的电势差与两点间的距离成正比,则E点的电势等于AD两点电势的平均值,F的电势等于BC两点电势的平均值,根据电场力公式W=qU,可得到WMN与WAB、WDC的关系.由于电场强度方向未知,不能求解场强的大小.由公式W=qU,可求出M、N间电势差
解答 解:A、将粒子从D点移动到C点,电场力做功为:WDC=3.2×10-8J,故:UDC=$\frac{{W}_{DC}}{q}$=$\frac{2.4×1{0}^{-8}}{2.4×1{0}^{-8}}$=1V,故A正确;
B、若带正电的粒子从A 点移动到B点,电场力做功为WAB=0.8×lO-8J,故:UAB=$\frac{{W}_{AB}}{q}$=$\frac{0.8×1{0}^{-8}}{0.8×1{0}^{-8}}$=1V,由于公式U=Ed中d表示沿着电场线方向的距离,故B错误;
C、D、因为电场是匀强电场,在同一条电场线上,E点的电势是A、D两点电势的平均值;F点的电势是B、C两点电势的平均值,故:φE=$\frac{{φ}_{A}+{φ}_{D}}{2}$,φF=$\frac{{φ}_{B}+{φ}_{C}}{2}$;
若将该粒子从E点移动到F点,电场力做功为:WEF=q(φE-φF)=q×$\frac{1}{2}$[(φA-φB)+(φD-φC)]=q×$\frac{1}{2}$×(UAB+UDC)=$\frac{1}{2}$(WAB+WDC)=$\frac{1}{2}$×(1.6×lO-8J+3.2×lO-8J)=2.4×lO-8J,故C错误,D正确;
故选:AD
点评 本题关键抓住E、F的电势与A、B电势和D、C电势的关系,根据电场力做功公式求解WEF.运用公式U=Ed时,要正确理解d的含义:d是沿电场方向两点间的距离.

 如图所示,O1O2是矩形线框的对称轴,左半部分处于匀强磁场中,下列哪些情况能让线框abcd中产生感应电流,且感应电流方向为a→b→c→d→a( )
如图所示,O1O2是矩形线框的对称轴,左半部分处于匀强磁场中,下列哪些情况能让线框abcd中产生感应电流,且感应电流方向为a→b→c→d→a( )| A. | 将线框向纸内平移 | B. | 将线框以cd为轴转动60° | ||
| C. | 将线框向左平移 | D. | 将线框以ab为轴转动30° |
| 器 材 | 规 格 | 器 材 | 规 格 |
| 小灯泡 | 标有“3.8V,0.3V”字样 | 滑动变阻器R1 | 最大阻值10Ω,额定电流1.0A |
| 电压表V | 量程0-5V,内阻5kΩ | 滑动变阻器R2 | 最大阻值1kΩ,额定电流0.5A |
| 电流表A1 | 量程0-100mA,内阻4Ω | 直流电源E | 电动势约6V,内阻约为0.5Ω |
| 电流表A2 | 量程0-500mA,内阻0.4Ω | 导线、电键等 |

①在上述器材中,滑动变阻器应选${R}_{1}^{\;}$.
②在图甲中用笔画线代替导线,把实验仪器连接成完整的实验电路.
③利用实验中得到的实验数据在I-U坐标系中,描绘出了图乙所示的小灯泡的伏安特性曲线.根据此图给出的信息,可以判断出图丙中正确的是(图中P为小灯泡功率)D.
 2015年莫斯科世锦赛上,我国男子短道速滑队时隔15年再次站到5000m接力的冠军领奖台上.观察发现,“接棒”的运动员甲提前站在“交棒”的运动员乙前面,并且开始向前滑行,待乙追上甲时,乙猛推甲,甲获得更大的速度向前冲出.在乙推甲的过程中,忽略运动员与冰面间在水平方向上的相互作用,则( )
2015年莫斯科世锦赛上,我国男子短道速滑队时隔15年再次站到5000m接力的冠军领奖台上.观察发现,“接棒”的运动员甲提前站在“交棒”的运动员乙前面,并且开始向前滑行,待乙追上甲时,乙猛推甲,甲获得更大的速度向前冲出.在乙推甲的过程中,忽略运动员与冰面间在水平方向上的相互作用,则( )| A. | 甲对乙的作用力与乙对甲的作用力相同 | |
| B. | 甲对乙的作用力一定做正功,乙的动能增大 | |
| C. | 乙对甲的作用力一定做正功,甲的动能增大 | |
| D. | 甲的动能增加量一定等于乙的动能减少量 |
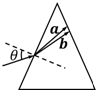 在玻璃中有一个截面为三角形的柱状真空空腔,a、b两束单色光以同样的入射角θ由玻璃射入空腔,部分光路如图,下列说法正确的是( )
在玻璃中有一个截面为三角形的柱状真空空腔,a、b两束单色光以同样的入射角θ由玻璃射入空腔,部分光路如图,下列说法正确的是( )| A. | 若增大θ,b光在空腔内先消失 | |
| B. | 若改变θ,a光通过空腔的时间一定比b光短 | |
| C. | 在同一双缝干涉装置上的干涉条纹a光较宽 | |
| D. | 若将两个相同的小球分别涂上a、b两种颜色放在同样深度的水中,在水面上看涂a颜色的小球较浅 |
| A. | 轮缘对外轨的侧压力减小 | B. | 轮缘对内轨侧压力增大 | ||
| C. | 轮缘对内、外轨无侧压力 | D. | 轮缘对外轨侧压力增大 |
 如图所示,平行金属板长为L,一个带电为+q质量为m的粒子以初速度v0紧贴上板垂直射入电场,刚好从下板边缘射出,末速度恰与下板成60°角,粒子重力不计,求:
如图所示,平行金属板长为L,一个带电为+q质量为m的粒子以初速度v0紧贴上板垂直射入电场,刚好从下板边缘射出,末速度恰与下板成60°角,粒子重力不计,求: 如图,水平面内有一光滑金属导轨,其MN、PQ边的电阻不计,MP边的电阻阻值R=1Ω,MN与MP的夹角为127°,PQ与MP垂直,MP边长度等于1m.将质量m=2kg,电阻不计的足够长直导体棒搁在导轨上,并与MP平行.棒与MN、PQ交点G、H间的距离L1=5m,E、F间的距离L2=2m.空间存在垂直于导轨平面的匀强磁场,磁感应强度B=0.1T.在外力作用下,棒由GH处以一定的初速度向左做直线运动,运动时回路中的电流强度始终与初始时的电流强度相等.(sin37°=0.6;cos37°=0.8)
如图,水平面内有一光滑金属导轨,其MN、PQ边的电阻不计,MP边的电阻阻值R=1Ω,MN与MP的夹角为127°,PQ与MP垂直,MP边长度等于1m.将质量m=2kg,电阻不计的足够长直导体棒搁在导轨上,并与MP平行.棒与MN、PQ交点G、H间的距离L1=5m,E、F间的距离L2=2m.空间存在垂直于导轨平面的匀强磁场,磁感应强度B=0.1T.在外力作用下,棒由GH处以一定的初速度向左做直线运动,运动时回路中的电流强度始终与初始时的电流强度相等.(sin37°=0.6;cos37°=0.8)