题目内容
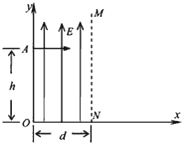如图所示，在空间中取直角坐标系Oxy，在第一象限内平行于y轴的虚线MN与y轴距离为d，从y轴到MN之间的区域充满一个沿y轴正方向的匀强电场，场强大小为E．初速可忽略的电子经过一个电势差U未确定的电场直线加速后，从y轴上的A点以垂直于电场的方向射入第一象限区域，A点坐标为（0，h），已知电子的电量为e，质量为m，（重力忽略不计），若电子可以在第一象限从MN边界离开电场区域，求：（1）加速电场的电势差要满足的条件；
（2）若满足上述条件的加速电场的电势差为U0时，求电子经过x轴时离坐标原点O的距离X．
分析：（1）根据动能定理求出电子由加速电场获得的速度．电子进入图中电场时，做类平抛运动，水平方向做匀速直线运动，竖直方向做初速度为零的匀加速运动，由牛顿第二定律和运动学公式结合求出电子离开电场距离x，当x＞d，电子离开有界电场．
（2）电子离开电场后做匀速直线运动，分别求出水平和竖直两个方向的位移，再求解电子经过x轴时离坐标原点O的距离X．
（2）电子离开电场后做匀速直线运动，分别求出水平和竖直两个方向的位移，再求解电子经过x轴时离坐标原点O的距离X．
解答：解：（1）以电子为研究对象，受力分析知，电子进入图中电场时，做类平抛运动，水平方向做匀速直线运动，竖直方向做初速度为零的匀加速运动．
进入电场前，设加速电压为U，进入电场的速度为v0，在电场运动的时间为t，由动能定理得：
eU=
mv02…①
进入电场后，电子做类平抛运动
所以 x=v0t…②
y=
at2…③
a=
…④
当电子离开电场时，x＞d..⑤
联立①②③④⑤解得：U＞
（2）当电子离开电场后，做匀速直线运动．运动轨迹如图所示．
设离开电场的夹角为θ，所以tanθ=
=
=
电子在电场的偏转距离 y=
=
(
)2=
电子出电场后由图可知：Y=h-y=h-
电子经过x轴时离坐标原点O的距离X为：X=d+Ycotθ=
+
答：（1）加速电场的电势差要满足的条件为U＞
；
（2）若满足上述条件的加速电场的电势差为U0时，求电子经过x轴时离坐标原点O的距离X为
+
．
．
进入电场前，设加速电压为U，进入电场的速度为v0，在电场运动的时间为t，由动能定理得：
eU=
| 1 |
| 2 |
进入电场后，电子做类平抛运动
所以 x=v0t…②
y=
| 1 |
| 2 |
a=
| Ee |
| m |
当电子离开电场时，x＞d..⑤
联立①②③④⑤解得：U＞
| Ed2 |
| 4h |
（2）当电子离开电场后，做匀速直线运动．运动轨迹如图所示．
设离开电场的夹角为θ，所以tanθ=
| vy |
| v0 |
| at |
| v0 |
| Ed |
| 2U0 |
电子在电场的偏转距离 y=
| at2 |
| 2 |
| Ee |
| 2m |
| d |
| v 0 |
| Ed2 |
| 4U0 |
电子出电场后由图可知：Y=h-y=h-
| Ed2 |
| 4U0 |
电子经过x轴时离坐标原点O的距离X为：X=d+Ycotθ=
| d |
| 2 |
| 2hU0 |
| Ed |
答：（1）加速电场的电势差要满足的条件为U＞
| Ed2 |
| 4h |
（2）若满足上述条件的加速电场的电势差为U0时，求电子经过x轴时离坐标原点O的距离X为
| d |
| 2 |
| 2hU0 |
| Ed |
．
点评：本题是带电粒子在匀强电场中偏转问题，明确电子的运动情况和遵循的规律即运用运动的分解法研究．
练习册系列答案
相关题目
（2010?浙江模拟）如图所示，在空间中取直角坐标系Oxy，在第一象限内平行于y轴的虚线MN与y轴距离为d，从y轴到MN之间的区域充满一个沿y轴正方向的匀强电场，场强大小为E．初速度可以忽略的电子经过另一个电势差为U的电场加速后，从y轴上的A点以平行于x轴的方向射入第一象限区域，A点坐标为（0，h）．已知电子的电量为e，质量为m，加速电场的电势差U＞
如图所示，在空间中取正交坐标系Oxyz（仅画出正半轴），沿x轴有一无限长通电直导线，电流沿x轴正方向，一束电子（重力不计）沿y=0，z=2的直线上（图中虚线所示）作匀速直线运动，方向也向x轴正方向，下列分析可以使电子完成以上运动的是（ ）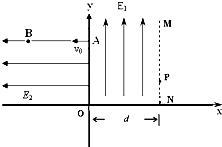
如图所示，在空间中取直角坐标系xOy，在第一象限内从y轴到MN之间的区域充满一个沿y轴正方向的匀强电场，MN为电场的理想边界，场强大小为E1，ON=d．在第二象限内充满一个沿x轴负方向的匀强电场，场强大小为E2．电子从y轴上的A点以初速度v0沿x轴负方向射入第二象限区域，它到达的最右端为图中的B点，之后返回第一象限，且从MN上的P点离开．已知A点坐标为（0，h）．电子的电量为e，质量为m，电子的重力忽略不计，求：
，电子的重力忽略不计，求：