题目内容
一质量为m的探月卫星绕月球转一圈的最短时间为t，根据常量和前述数据可求得月球的（ ）
| A．质量 | B．半径 |
| C．密度 | D．第一宇宙速度 |
设月球的质量为M，半径R，第一宇宙速度为v．
根据开普勒第三定律可知探月卫星绕表面附近运行时周期最小，且速度最大，即为第一宇宙速度．
由题得最小周期为 T=t
对于探月卫星，根据万有引力提供向心力得：
G
=m
R=m
则得：M=
，v=
，可以看出不能求出R，就不能求出M和v，即求不出月球的质量和第一宇宙速度．
月球的密度 ρ=
=
=
=
，可知能求出月球的密度．故ABD错误，C正确．
故选：C
根据开普勒第三定律可知探月卫星绕表面附近运行时周期最小，且速度最大，即为第一宇宙速度．
由题得最小周期为 T=t
对于探月卫星，根据万有引力提供向心力得：
G
| Mm |
| R2 |
| 4π2 |
| T2 |
| v2 |
| R |
则得：M=
| 4π2R3 |
| GT2 |
|
月球的密度 ρ=
| M | ||
|
| ||
|
| 3π |
| GT2 |
| 3π |
| Gt2 |
故选：C
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
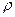，靠近行星表面的卫星，其运行周期为T，试证明
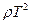为一常数。