Question

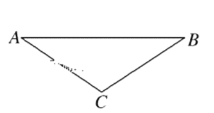
【题目】如图所示，一根绳的两端分别固定在两座猴山的A、B处，A、B两点水平距离为16m，竖直距离为2m，A、B间绳长为20m．质量为10kg的猴子抓住套在绳上的滑环从A处滑到B处。以A点所在水平面为参考平面，猴子在滑行过程中重力势能最小值约为(绳处于拉直状态) ( )

A.B.

C.D.

Answer 1

【答案】A

【解析】

猴子的动能最大时重力势能最小，猴子的加速度为零时速度最大，动能最大，此时猴子受力平衡则可以得到下面的几何关系：

绳长AC+BC=AF=20m，又MF=16m，由勾股定理得AM=12m，而AB竖直距离为2m，则BF=10m，D为BF中点，BD=5m，C和D等高，则A、C的竖直高度差为7m，此时猴子的重力势能为：

A. 与上述计算结果-700J接近，故A符合题意；

B. 与上述计算结果-700J相差较大，故B不符合题意；

C. 与上述计算结果-700J相差较大，故C不符合题意；

D. 与上述计算结果-700J相差较大，故D不符合题意。