题目内容
14. 如图所示是一个透明圆柱体的横截面,一束单色光平行于直径AB射向圆柱体,光线经过折射后恰能射到B点.已知透明介质对单色光的折射率为n=$\sqrt{3}$,横截面的半径为R,光在真空中的传播速度为c,求:
如图所示是一个透明圆柱体的横截面,一束单色光平行于直径AB射向圆柱体,光线经过折射后恰能射到B点.已知透明介质对单色光的折射率为n=$\sqrt{3}$,横截面的半径为R,光在真空中的传播速度为c,求:①光在介质中运动的时间;
②平行光线到直径AB的距离d.
分析 ①画出光路图,由折射定律得到入射角与折射角的关系,由几何关系也得到入射角与折射角的关系,即可求出入射角与折射角,再根据几何知识求解这条入射光线在透明圆柱体中传播的距离s,根据公式v=$\frac{c}{n}$求光在该透明圆柱体中的传播速度,再由t=$\frac{s}{v}$求时间.
②由几何知识求平行光线到直径AB的距离d.
解答  解:①根据题意作出光路图,如图所示,折射率n=$\frac{sinα}{sinβ}$=$\sqrt{3}$
解:①根据题意作出光路图,如图所示,折射率n=$\frac{sinα}{sinβ}$=$\sqrt{3}$
又由几何关系知α=2β,解得α=60°,β=30°
根据几何关系可求 BC=2Rcosβ=$\sqrt{3}$R,光在介质中的传播速度为 v=$\frac{c}{n}$=$\frac{c}{\sqrt{3}}$
故光在介质中传播的时间为:t=$\frac{BC}{v}$=$\frac{3R}{c}$
②如图所示光线到AB的距离为CD,在三角形BCD中可求得 CD=$\frac{1}{2}$BC,所以 d=CD=$\frac{\sqrt{3}}{2}$R
答:
①光在介质中运动的时间为$\frac{3R}{c}$;
②平行光线到直径AB的距离d是$\frac{\sqrt{3}}{2}$R.
点评 对于几何光学问题,首先要正确作出光路图,其次要运用几何知识分析入射角与折射角的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.关于匀速圆周运动的角速度、线速度、周期和频率的说法,正确的是( )
| A. | 角速度与线速度成正比 | B. | 角速度与周期成反比 | ||
| C. | 线速度与周期成正比 | D. | 角速度与频率成反比 |
5.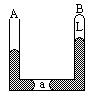 A端开口,B端封闭的粗细均匀的U型玻璃管,注入水银后有a、b两段空气被密封如图所示,设外界大气压不变,今使整个U型管的温度升高( )
A端开口,B端封闭的粗细均匀的U型玻璃管,注入水银后有a、b两段空气被密封如图所示,设外界大气压不变,今使整个U型管的温度升高( )
 A端开口,B端封闭的粗细均匀的U型玻璃管,注入水银后有a、b两段空气被密封如图所示,设外界大气压不变,今使整个U型管的温度升高( )
A端开口,B端封闭的粗细均匀的U型玻璃管,注入水银后有a、b两段空气被密封如图所示,设外界大气压不变,今使整个U型管的温度升高( )| A. | A端水银上升,B端水银下降 | |
| B. | A、B两端水银面都上升,但水银面高度差变小 | |
| C. | A、B两端水银面都上升,但水银面高度差变大 | |
| D. | A、B两端水银面都上升,但水银面高度差不变 |
2. 如图为竖直放置的上细下粗的密闭细管,水银柱将气体分隔成A、B两部分,初始温度相同.使A、B升高相同温度达到稳定后,体积变化量为△VA、△VB,压强变化量为△pA、△pB,对液面压力的变化量为△FA、△FB,则下列叙述不正确的是( )
如图为竖直放置的上细下粗的密闭细管,水银柱将气体分隔成A、B两部分,初始温度相同.使A、B升高相同温度达到稳定后,体积变化量为△VA、△VB,压强变化量为△pA、△pB,对液面压力的变化量为△FA、△FB,则下列叙述不正确的是( )
 如图为竖直放置的上细下粗的密闭细管,水银柱将气体分隔成A、B两部分,初始温度相同.使A、B升高相同温度达到稳定后,体积变化量为△VA、△VB,压强变化量为△pA、△pB,对液面压力的变化量为△FA、△FB,则下列叙述不正确的是( )
如图为竖直放置的上细下粗的密闭细管,水银柱将气体分隔成A、B两部分,初始温度相同.使A、B升高相同温度达到稳定后,体积变化量为△VA、△VB,压强变化量为△pA、△pB,对液面压力的变化量为△FA、△FB,则下列叙述不正确的是( )| A. | 水银柱向上移动了一段距离 | B. | 水银柱向下移动了一段距离 | ||
| C. | △VA<△VB | D. | △pA>△pB | ||
| E. | △FA=△FB |
9.下列说法正确的是( )
| A. | 只有物体温度较高时,才能向外辐射红外线 | |
| B. | 紫外线的主要作用是化学作用和荧光作用 | |
| C. | 可见光比红外线容易发生衍射现象 | |
| D. | X射线能在磁场中偏转,穿透力较强,可用来进行人体透视 |
3.汽车从静止开始沿平直公路做匀加速运动,所受阻力始终不变.在此过程中,下列说法正确的是( )
| A. | 汽车发动机的牵引力随时间均匀增大 | |
| B. | 汽车发动机的输出功率随时间均匀增大 | |
| C. | 汽车发动机做的功等于汽车动能的增加量 | |
| D. | 在任意两段相等的位移内汽车速度的变化量相等 |
4. 如图所示,a、b为两等量异号点电荷,cd为ab连线的中垂线.一带有微量正电的点电荷A以一定的初速度沿cd方向射入电场,其运动轨迹为图中虚线,交ab于e.不计重力.则( )
如图所示,a、b为两等量异号点电荷,cd为ab连线的中垂线.一带有微量正电的点电荷A以一定的初速度沿cd方向射入电场,其运动轨迹为图中虚线,交ab于e.不计重力.则( )
 如图所示,a、b为两等量异号点电荷,cd为ab连线的中垂线.一带有微量正电的点电荷A以一定的初速度沿cd方向射入电场,其运动轨迹为图中虚线,交ab于e.不计重力.则( )
如图所示,a、b为两等量异号点电荷,cd为ab连线的中垂线.一带有微量正电的点电荷A以一定的初速度沿cd方向射入电场,其运动轨迹为图中虚线,交ab于e.不计重力.则( )| A. | a带负电荷 | B. | A的运动轨迹为抛物线 | ||
| C. | 电场强度Ec>Ee | D. | 电势φc>φe |
 甲、乙两质点在同一时刻、从同一地点沿同一方向做直线运动.甲做初速度为v0,加速度大小为a1的匀减速直线运动,速度减为零后保持静止,乙做初速度为零,加速度大小为a2的匀加速直线运动.甲、乙在运动过程中的位移-速度平方(x-v2)图象如图所示,虚线与对应的坐标轴垂直,请利用图中数据,求
甲、乙两质点在同一时刻、从同一地点沿同一方向做直线运动.甲做初速度为v0,加速度大小为a1的匀减速直线运动,速度减为零后保持静止,乙做初速度为零,加速度大小为a2的匀加速直线运动.甲、乙在运动过程中的位移-速度平方(x-v2)图象如图所示,虚线与对应的坐标轴垂直,请利用图中数据,求