题目内容
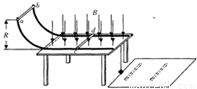
如图所示,电阻不计的两光滑金属导轨相距L放在水平绝缘桌面上,半径为R的 圆弧部分处在竖直平面内,水平直导轨部分处在磁感应强度为B、方向竖直向下的匀强磁场中,末端与桌面边缘平齐.两金属棒ab、cd垂直两导轨且与导轨接触良好,ab棒质量为2m、电阻为r,cd棒质量为m、电阻为r.开始时cd棒静止在水平直导轨上,ab棒从圆弧导轨的顶端无初速释放,进入水平直 导轨后与cd棒始终没有接触并一直向右运动,最后两棒都离开导轨落到地面上.两棒落地点到桌面边缘的水平距离之比为3:1,求:
圆弧部分处在竖直平面内,水平直导轨部分处在磁感应强度为B、方向竖直向下的匀强磁场中,末端与桌面边缘平齐.两金属棒ab、cd垂直两导轨且与导轨接触良好,ab棒质量为2m、电阻为r,cd棒质量为m、电阻为r.开始时cd棒静止在水平直导轨上,ab棒从圆弧导轨的顶端无初速释放,进入水平直 导轨后与cd棒始终没有接触并一直向右运动,最后两棒都离开导轨落到地面上.两棒落地点到桌面边缘的水平距离之比为3:1,求:(1)cd棒在水平直导轨上的最大加速度.
(2)两棒在导轨上运动的过程中产生的焦耳热.
【答案】分析:(1)ab棒刚进入水平导轨时,cd棒受到的安培力最大,此时它的加速度最大.根据ab棒从圆弧导轨滑下机械能定恒求解进入磁场之前的速度大小,由E=BLv、I=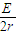 、F=BIL结合求出安培力,即可由牛顿第二定律求解最大加速度.
、F=BIL结合求出安培力,即可由牛顿第二定律求解最大加速度.
(2)ab棒与cd棒在水平导轨上运动,根据动量定恒和两棒离开导轨做平抛运动的时间相等求出棒ab和棒cd离开导轨时的速度大小;根据能量定恒求解两棒在轨道上运动过程产生的焦耳热.
解答:解:(1)ab棒刚进入水平导轨时,cd棒受到的安培力最大,此时它的加速度最大.
设ab棒进入水平导轨的速度为v1,ab棒从圆弧导轨滑下机械能定恒:
2mgR= ×2mv12
×2mv12
解得:v1=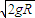 . ①
. ①
ab棒刚进入水平导轨时,设此时回路的感应电动势为E,
E=BLv ③
I=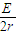 ④
④
cd棒受到的安培力为:Fcd=BIL ⑤
根据牛顿第二定律,cd棒有最大加速度为
a=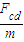 ⑥
⑥
联立①~⑥解得:
a=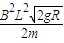 ⑦
⑦
(2)离开导轨时,设ab棒的速度为v1′,cd棒的速度为v2′,ab棒与cd棒在水平导轨上运动,根据动量定恒得:
2mv1=2mv1′+mv2′⑧
依题意v1′>v2′,⑨
两棒离开导轨做平抛运动的时间相等,
由平抛运动水平位移x=vt可知 v1′:v2′=x1:x2=1:3
解得,v1′=3v2′,⑩
根据能量定恒,两棒在轨道上运动过程产生的焦耳热为
Q=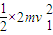 -(
-(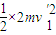 +
+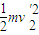 )(11)
)(11)
由①⑧⑩(11)解得,Q=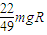
答:
(1)cd棒在水平直导轨上的最大加速度为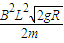 .
.
(2)两棒在导轨上运动的过程中产生的焦耳热为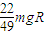 .
.
点评:本题是电磁感应与电路、磁场、力学等知识的综合应用,根据牛顿第二定律求加速度,以及结合运动学能够分析出金属棒的运动情况.
考查分析和处理综合题的能力.
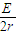 、F=BIL结合求出安培力,即可由牛顿第二定律求解最大加速度.
、F=BIL结合求出安培力,即可由牛顿第二定律求解最大加速度.(2)ab棒与cd棒在水平导轨上运动,根据动量定恒和两棒离开导轨做平抛运动的时间相等求出棒ab和棒cd离开导轨时的速度大小;根据能量定恒求解两棒在轨道上运动过程产生的焦耳热.
解答:解:(1)ab棒刚进入水平导轨时,cd棒受到的安培力最大,此时它的加速度最大.
设ab棒进入水平导轨的速度为v1,ab棒从圆弧导轨滑下机械能定恒:
2mgR=
 ×2mv12
×2mv12 解得:v1=
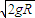 . ①
. ①ab棒刚进入水平导轨时,设此时回路的感应电动势为E,
E=BLv ③
I=
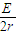 ④
④cd棒受到的安培力为:Fcd=BIL ⑤
根据牛顿第二定律,cd棒有最大加速度为
a=
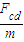 ⑥
⑥联立①~⑥解得:
a=
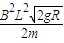 ⑦
⑦(2)离开导轨时,设ab棒的速度为v1′,cd棒的速度为v2′,ab棒与cd棒在水平导轨上运动,根据动量定恒得:
2mv1=2mv1′+mv2′⑧
依题意v1′>v2′,⑨
两棒离开导轨做平抛运动的时间相等,
由平抛运动水平位移x=vt可知 v1′:v2′=x1:x2=1:3
解得,v1′=3v2′,⑩
根据能量定恒,两棒在轨道上运动过程产生的焦耳热为
Q=
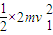 -(
-(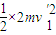 +
+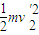 )(11)
)(11)由①⑧⑩(11)解得,Q=
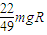
答:
(1)cd棒在水平直导轨上的最大加速度为
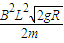 .
.(2)两棒在导轨上运动的过程中产生的焦耳热为
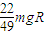 .
.点评:本题是电磁感应与电路、磁场、力学等知识的综合应用,根据牛顿第二定律求加速度,以及结合运动学能够分析出金属棒的运动情况.
考查分析和处理综合题的能力.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 如图所示,电阻不计的平行金属导轨MN和OP水平放置.MO间接有阻值为R的电阻.导轨相距为d,有竖直向下的匀强磁场,磁感强度为B.质量为m,长为L的导体棒CD的电阻为r,垂直于导轨放置,并接触良好.用平行于MN的恒力F向右拉动CD棒.CD棒受恒定的摩擦阻力f.已知F>f,L>d,求:
如图所示,电阻不计的平行金属导轨MN和OP水平放置.MO间接有阻值为R的电阻.导轨相距为d,有竖直向下的匀强磁场,磁感强度为B.质量为m,长为L的导体棒CD的电阻为r,垂直于导轨放置,并接触良好.用平行于MN的恒力F向右拉动CD棒.CD棒受恒定的摩擦阻力f.已知F>f,L>d,求: 如图所示,电阻不计的平行粗糙长金属导轨固定在一绝缘斜面上,两相同的金属棒a、b垂直于导轨放置,且与导轨良好接触,匀强磁场垂直穿过导轨平面.现用一平行于导轨的恒力F作用在a的中点,使其向上运动.在a运动的整个过程中若b始终保持静止,则它所受摩擦力可能( )
如图所示,电阻不计的平行粗糙长金属导轨固定在一绝缘斜面上,两相同的金属棒a、b垂直于导轨放置,且与导轨良好接触,匀强磁场垂直穿过导轨平面.现用一平行于导轨的恒力F作用在a的中点,使其向上运动.在a运动的整个过程中若b始终保持静止,则它所受摩擦力可能( ) 如图所示,电阻不计的平行金属导轨MN和OP放置在水平面内,MO间接有阻值为R=3Ω的电阻,导轨相距d=1m,其间有竖直向下的匀强磁场,磁感应强度B=0.5T.质量为m=0.1kg,电阻为r=1Ω的导体棒CD垂直于导轨放置,并接触良好.用平行于MN的恒力F=1N向右拉动CD,CD受摩擦阻力f恒为0.5N.求:(1)CD运动的最大速度;(2)当CD达到最大速度后,电阻R消耗的电功率.
如图所示,电阻不计的平行金属导轨MN和OP放置在水平面内,MO间接有阻值为R=3Ω的电阻,导轨相距d=1m,其间有竖直向下的匀强磁场,磁感应强度B=0.5T.质量为m=0.1kg,电阻为r=1Ω的导体棒CD垂直于导轨放置,并接触良好.用平行于MN的恒力F=1N向右拉动CD,CD受摩擦阻力f恒为0.5N.求:(1)CD运动的最大速度;(2)当CD达到最大速度后,电阻R消耗的电功率. (2013?河南模拟)如图所示,电阻不计的平行光滑金属导轨与水平面的夹角为θ,宽度为l,下端与阻值为R的电阻相连.磁感应强度为B的匀强磁场垂直穿过导轨平面,现使质量为m的导体棒ab位置以平行于斜面的初速度沿导轨向上运动,滑行到最远位置a′b′后又下湍.已知导体棒运动过程中的最大加速度为2gsinθ,g为重力加速度,轨道足够长,则( )
(2013?河南模拟)如图所示,电阻不计的平行光滑金属导轨与水平面的夹角为θ,宽度为l,下端与阻值为R的电阻相连.磁感应强度为B的匀强磁场垂直穿过导轨平面,现使质量为m的导体棒ab位置以平行于斜面的初速度沿导轨向上运动,滑行到最远位置a′b′后又下湍.已知导体棒运动过程中的最大加速度为2gsinθ,g为重力加速度,轨道足够长,则( ) (2012?湛江一模)如图所示,电阻不计的光滑平行金属导轨MN和OP水平放置,MO间接有阻值为R的电阻,两导轨相距为L,其间有竖直向下的匀强磁场.质量为m、长度为L、电阻为R0的导体棒CD垂直于导轨放置,并接触良好.在CD的中点处用大小为F平行于MN向右的水平恒力啦CD从静止开始运动s的位移,导体棒CD的速度恰好达到最大速度vm.
(2012?湛江一模)如图所示,电阻不计的光滑平行金属导轨MN和OP水平放置,MO间接有阻值为R的电阻,两导轨相距为L,其间有竖直向下的匀强磁场.质量为m、长度为L、电阻为R0的导体棒CD垂直于导轨放置,并接触良好.在CD的中点处用大小为F平行于MN向右的水平恒力啦CD从静止开始运动s的位移,导体棒CD的速度恰好达到最大速度vm.