题目内容
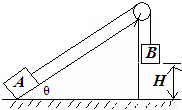
如图，已知斜面倾角30，物体A质量mA=0.4kg，物体B质量mB=0.7kg，H=0.5m．B从静止开始和A一起运动，B落地时速度v=2m/s．若g取10m/s2，绳的质量及绳的摩擦不计，求：（1）物体与斜面间的动摩擦因数
（2）物体沿足够长的斜面滑动的最大距离．
【答案】分析：（1）以AB组成的整体为研究对象，根据动能定理求出动摩擦因数．
（2）B落地时A的速度大小等于B的速度大小，再根据动能定理求解物体沿滑动的最大距离．
解答：解：（1）以AB组成的整体为研究对象，根据动能定理得：
mBgH-mAgsinθ?H-μmAgcosθ?H=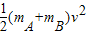
得：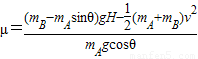
代入解得：μ=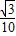
（2）设物体沿斜面滑动的最大距离为S，根据动能定理得
B落地后过程，对A：
-mAgsinθ?（S-H）-μmAgcosθ（S-H）=0-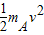
代入解得，S≈0.8m
答：
（1）物体与斜面间的动摩擦因数为μ=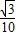
．
（2）物体沿足够长的斜面滑动的最大距离为0.8m．
点评：本题是连接体问题，运用动能定理进行处理．也可以根据牛顿第二定律和运动学结合研究．
（2）B落地时A的速度大小等于B的速度大小，再根据动能定理求解物体沿滑动的最大距离．
解答：解：（1）以AB组成的整体为研究对象，根据动能定理得：
mBgH-mAgsinθ?H-μmAgcosθ?H=
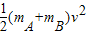
得：
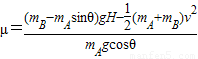
代入解得：μ=
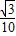
（2）设物体沿斜面滑动的最大距离为S，根据动能定理得
B落地后过程，对A：
-mAgsinθ?（S-H）-μmAgcosθ（S-H）=0-
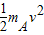
代入解得，S≈0.8m
答：
（1）物体与斜面间的动摩擦因数为μ=
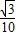．（2）物体沿足够长的斜面滑动的最大距离为0.8m．
点评：本题是连接体问题，运用动能定理进行处理．也可以根据牛顿第二定律和运动学结合研究．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，已知斜面倾角37°，物体A质量mA=0.4kg，物体B质量mB=0.6kg，H=1.0m．B从静止开始和A一起运动，B落地时速度v=2m/s．若g取10m/s2，绳的质量及绳的摩擦不计，求：
（2011?安庆二模）如图所示，斜面体B放在水平地面上，木块A放在斜面体B上，用一个沿斜面向上的力F拉木块A，在力F的作用下，物体A与斜面体B一起沿水平方向匀速移动，已知斜面倾角为θ，则关于斜面体B受力的个数，下面说法中正确的是（ ）
如图所示，斜面体B放在水平地面上，木块A放在斜面体B上，用一个沿斜面向上的力F拉木块A，在力F的作用下，木块A与斜面体B一起沿水平方向匀速移动，已知斜面倾角为θ，则关于斜面体B受力的个数，下面说法中正确的是（ ）| A、可能是3个 | B、可能是4个 | C、一定是5个 | D、可能是5个 |
如图，已知斜面倾角37°，物体A质量mA=0.4kg，物体B质量mB=0.6kg，H=1.0m．B从静止开始和A一起运动，B落地时速度v=2m/s．若g取10m/s2，绳的质量及绳的摩擦不计，求：