题目内容
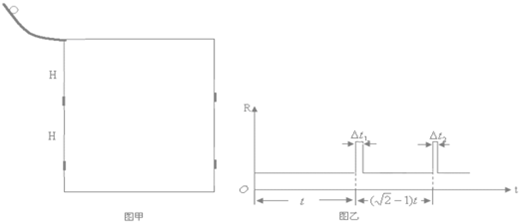
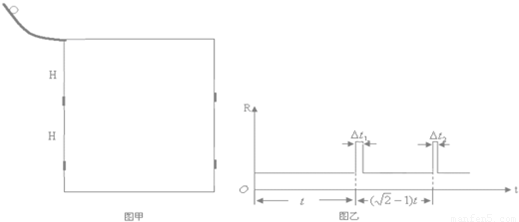
（20分）如图甲所示，在一对平行光滑的金属导轨的上端连接一阻值为R=4Ω的定值电阻，两导轨在同一平面内.质量为m=0.1kg，长为L=0.1m的导体棒ab垂直于导轨，使其从靠近电阻处由静止开始下滑，已知导体棒电阻为r=1Ω，整个装置处于垂直于导轨平面的匀强磁场中，导体棒下滑过程中加速度a与速度v的关系如图乙所示.（g=10m/s2）.求：
（1）导轨平面与水平面间夹角θ；
（2）磁场的磁感应强度B；
（3）若靠近电阻处到底端距离为x=20m，ab棒在下滑至底端前速度已达10m/s，求ab棒下滑的整个过程中，电阻R上产生的焦耳热.
（1）
(2) 
（3）
【解析】（20分） 解：（1）设刚开始下滑时导体棒的加速度为
，则
……………… （1分）
……………… （2分）
……………… （2分）
(2)当导体棒的加速度为零时，开始做匀匀速运动的速度为
，导体棒上的感应电动势为
，电路中的电流为
，则由图知：
……………………………………………
（1分）
此时，由受力平衡得
…………………
（2分）
由闭合电路欧姆定律得：
………………… （2分）
感应电动势
………………………………
（2分）
联立以上各式解得 ……………………………
（2分）
（3）设ab棒下滑的过程中，产生的热量为Q，电阻R上产生的热量为QR，则 
……………… （2分）
……………… （2分）
解得： ………………………………………… （2分）
本题考查的是导体棒在斜面轨道的磁场中的运动问题。对导体棒进行受力分析，分析其运动状态，列平衡方程，再根据闭合电路欧姆定律解出磁感应强度；ab棒下滑的过程中，产生的热量为Q，电阻R上产生的热量为QR,由能量守恒列方程解出
.
