题目内容
14. 在跳水比赛中,有一个单项是“3m跳板”,其比赛过程可简化为:运动员走上跳板,再经过几次运动后运动员在跳板的水平点B获得2m/s的竖直向下的初速度,直到跳板被压缩到最低点C,接着跳板将运动员竖直向上弹到最高点,运动员做自由落体运动,竖直落入水中,将运动员视为质点,运动员质量m=50kg,g=10m/s,最高点A、跳板的水平点B、最低点C和水面之间的竖直距离如图所示.求:
在跳水比赛中,有一个单项是“3m跳板”,其比赛过程可简化为:运动员走上跳板,再经过几次运动后运动员在跳板的水平点B获得2m/s的竖直向下的初速度,直到跳板被压缩到最低点C,接着跳板将运动员竖直向上弹到最高点,运动员做自由落体运动,竖直落入水中,将运动员视为质点,运动员质量m=50kg,g=10m/s,最高点A、跳板的水平点B、最低点C和水面之间的竖直距离如图所示.求:(1)跳板被压缩到最低点C时,跳板的弹性势能以及运动员被弹起的高度hAC;
(2)运动员入水前速度大小.
分析 (1)设最低点C势能为零,运动员从B到C过程中,运动员的动能和势能转化为C点的弹性势能,根据能量守恒定律,求得C点的弹性势能,C到A过程弹性势能又转化为重力势能,根据能量守恒定律,求得AC的高度差.
(2)运动员从最高点到入水过程中,运用机械能守恒,列式即可求得水前速度大小.
解答 解:(1)运动员在B点时的动能为:${E}_{K}=\frac{1}{2}m{v}^{2}=\frac{1}{2}×50×{2}^{2}=100J$,势能为:EP=mghBC=50×10×0.8=400J,
根据能量守恒定律,B点的动能和势能转化为C点的弹性势能,故:EPC=EK+EP=100J+400J=500J,
C到A过程弹性势能又转化为重力势能,根据能量守恒定律有:EPC=EPA=mghAC,解得:hAC=1m,
(2)最高点与水面之间运动员做自由落体运动,设最高点与水面之间的高度差为H,则有:
H=hAC-hBC+hB水=1m-0.8m+3 m=3.2 m
运动员做自由落体运动,设运动员入水前的速度为v,则有:
v=$\sqrt{2gH}$
得:v=$\sqrt{2×10×3.2}$m/s=8m/s
答:(1)跳板被压缩到最低点C时,跳板的弹性势能为500J,运动员被弹起的高度hAC为3.2m;
(2)运动员入水前速度大小为8m/s.
点评 解答本题的关键知道运动员运动过程中那些能量之间进行转化,能正确运用能量守恒定律分析解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.某人站在一星球上,以速度v0竖直向上抛一小球,经t秒后,球落回手中,已知该星球半径为R,现将此球沿此星球表面将小球水平抛出,欲使其不落回星球,则抛出时的速度至少为( )
| A. | $\frac{v_0}{t}$ | B. | $\sqrt{\frac{{{v_0}R}}{t}}$ | C. | $\sqrt{\frac{{2{v_0}R}}{t}}$ | D. | $\sqrt{\frac{v_0}{Rt}}$ |
9. 如图所示,长为a宽为b的矩形区域内(包括边界)有磁感应强度为B的匀强磁场,磁场方向垂直纸面向外.0点有一粒子源,某时刻粒子源向磁场所在区域与磁场垂直的平面内所有方向发射大量质量为m电量为q的带正电的粒子,粒子的速度大小相同,粒子在磁场中做匀速圆周运动的周期为T,最先从磁场上边界射出的粒子经历的时间为$\frac{T}{12}$,最后从磁场中飞出的粒子经历的时间为$\frac{T}{4}$,不计重力和粒子之间的相互作用,则( )
如图所示,长为a宽为b的矩形区域内(包括边界)有磁感应强度为B的匀强磁场,磁场方向垂直纸面向外.0点有一粒子源,某时刻粒子源向磁场所在区域与磁场垂直的平面内所有方向发射大量质量为m电量为q的带正电的粒子,粒子的速度大小相同,粒子在磁场中做匀速圆周运动的周期为T,最先从磁场上边界射出的粒子经历的时间为$\frac{T}{12}$,最后从磁场中飞出的粒子经历的时间为$\frac{T}{4}$,不计重力和粒子之间的相互作用,则( )
 如图所示,长为a宽为b的矩形区域内(包括边界)有磁感应强度为B的匀强磁场,磁场方向垂直纸面向外.0点有一粒子源,某时刻粒子源向磁场所在区域与磁场垂直的平面内所有方向发射大量质量为m电量为q的带正电的粒子,粒子的速度大小相同,粒子在磁场中做匀速圆周运动的周期为T,最先从磁场上边界射出的粒子经历的时间为$\frac{T}{12}$,最后从磁场中飞出的粒子经历的时间为$\frac{T}{4}$,不计重力和粒子之间的相互作用,则( )
如图所示,长为a宽为b的矩形区域内(包括边界)有磁感应强度为B的匀强磁场,磁场方向垂直纸面向外.0点有一粒子源,某时刻粒子源向磁场所在区域与磁场垂直的平面内所有方向发射大量质量为m电量为q的带正电的粒子,粒子的速度大小相同,粒子在磁场中做匀速圆周运动的周期为T,最先从磁场上边界射出的粒子经历的时间为$\frac{T}{12}$,最后从磁场中飞出的粒子经历的时间为$\frac{T}{4}$,不计重力和粒子之间的相互作用,则( )| A. | 粒子速度大小为$\frac{qBb}{m}$ | |
| B. | 粒子做圆周运动的半径为3b | |
| C. | a的长度为($\sqrt{3}$+1)b | |
| D. | 最后从磁场中飞出的粒子一定从上边界的中点飞出 |
11. 如图所示,匀强电场方向竖直向上,质量相同的两个小球A、B以相同的初速度水平抛出,它们最后落在同一点上,它们中有一个带电,则( )
如图所示,匀强电场方向竖直向上,质量相同的两个小球A、B以相同的初速度水平抛出,它们最后落在同一点上,它们中有一个带电,则( )
 如图所示,匀强电场方向竖直向上,质量相同的两个小球A、B以相同的初速度水平抛出,它们最后落在同一点上,它们中有一个带电,则( )
如图所示,匀强电场方向竖直向上,质量相同的两个小球A、B以相同的初速度水平抛出,它们最后落在同一点上,它们中有一个带电,则( )| A. | 它们下落的时间tA>tB | |
| B. | 如果是A球带电,则A球带正电 | |
| C. | 如果是A球带电,A球下落时电势能减少 | |
| D. | 如果是B球带电,则B球只能带正电 |
8.如图,A、B是相同的白炽灯,L是自感系数很大、电阻可忽略的自感线圈.下面说法正确的是( )


| A. | 闭合开关S时,A、B灯同时亮,且达到正常 | |
| B. | 闭合开关S时,B灯比A灯先亮,最后一样亮 | |
| C. | 闭合开关S时,A灯比B灯先亮,最后A灯比B灯更亮 | |
| D. | 断开开关S时,A灯与B灯同时慢慢熄灭 |
 如图所示,绝缘斜面固定在水平地面上,斜面所在空间存在竖直向下的匀强电场.一带负电荷的滑块以初速度v0沿斜面上滑.已知滑块始终在斜面上运动,下面四个图象分别表示滑块运动过程中的速度-时间图象,其中可能正确的是( )
如图所示,绝缘斜面固定在水平地面上,斜面所在空间存在竖直向下的匀强电场.一带负电荷的滑块以初速度v0沿斜面上滑.已知滑块始终在斜面上运动,下面四个图象分别表示滑块运动过程中的速度-时间图象,其中可能正确的是( )



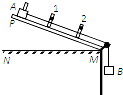 如图所示,NM是水平桌面,PM是一端带有滑轮的长木板,1、2是固定在木板上的两个光电门.质量为M的滑块A上固定一遮光条,在质量为m的重物B牵引下从木板的顶端由静止滑下,光电门1、2记录遮光时间分别为△t1和△t2.(重力加速度为g)
如图所示,NM是水平桌面,PM是一端带有滑轮的长木板,1、2是固定在木板上的两个光电门.质量为M的滑块A上固定一遮光条,在质量为m的重物B牵引下从木板的顶端由静止滑下,光电门1、2记录遮光时间分别为△t1和△t2.(重力加速度为g) 如图所示,足够长的两面均光滑的绝缘平板,固定在区域足够大的正交的方向竖直向上的匀强电场和方向水平向外的匀强磁场中,匀强电场的场强大小为E,匀强磁场的磁感强度大小为B,平板与水平面间的夹角为θ,带电荷量为+q的小物块静止在平板中央,现沿平板斜向下的方向给物块一个瞬时速度v0的同时,保持磁场(包括大小和方向)和电场的方向不变,使电场强度的大小变为3E(当地重力加速度为g),设物块沿平板运动的过程中电荷量不变),求:
如图所示,足够长的两面均光滑的绝缘平板,固定在区域足够大的正交的方向竖直向上的匀强电场和方向水平向外的匀强磁场中,匀强电场的场强大小为E,匀强磁场的磁感强度大小为B,平板与水平面间的夹角为θ,带电荷量为+q的小物块静止在平板中央,现沿平板斜向下的方向给物块一个瞬时速度v0的同时,保持磁场(包括大小和方向)和电场的方向不变,使电场强度的大小变为3E(当地重力加速度为g),设物块沿平板运动的过程中电荷量不变),求: 如图,小球质量为m,一不可伸长的悬线长为l,把悬线拉到水平位置后释放,小球在最低点所受拉力为F,不计空气阻力,则小球从水平位置A到竖直位置B的过程中,
如图,小球质量为m,一不可伸长的悬线长为l,把悬线拉到水平位置后释放,小球在最低点所受拉力为F,不计空气阻力,则小球从水平位置A到竖直位置B的过程中,