题目内容
在方向水平的匀强电场中，绝缘细线的一端连着一个质量为m的带电小球，另一端悬挂于O点。将小球拿到A点（此时细线与电场方向平行）无初速释放，已知小球摆到B点时速度为零，此时细线与竖直方向的夹角为θ=30°，求：
（1）小球速度最大的位置。
（2）小球速度最大时细线对小球的拉力。
（1）α=30°（2）
mg
解析试题分析：（1）小球由A运动到B根据动能定理，
mgLcosθ-qEL（1+sinθ）="0"
解得
设小球最大速度的位置为C，悬线与竖直方向间的夹角为
α，小球受力如图，则tanα=
=
，α=30°
（2）由A到C，根据动能定理，有mgLsin60°-qEL（1-cos60°）= 
在C点，根据牛顿第二定律，有
解得 T=mg
考点：动能定理及牛顿第二定律。
练习册系列答案
相关题目
的 1/4光滑圆弧轨道最低点D与水平面相切，在D点右侧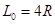
处用长为
的小球B（可视为质点）悬挂于O点，小球B的下端恰好与水平面接触，质量为
,细绳的最大张力
,重力加速度为
，试求：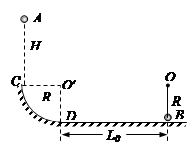
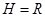，小球A到达圆弧轨道最低点D时所受轨道的支持力；
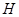在什么范围内，小球A与B发生弹性碰撞后细绳始终处于拉直状态。
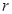为0.2m，在圆心O处固定一个电荷量为-
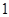.0×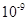
C的点电荷。质量为0.06kg、略小于圆管截面的带电小球,从与O点等高的A点沿圆管内由静止运动到最低点B ,到达B点小球刚好与圆弧没有作用力，然后从B点进入板距d= 0.08m的两平行板电容器后刚好能在水平方向上做匀速直线运动,且此时电路中的电动机刚好能正常工作。已知电源的电动势为12V,内阻为1Ω,定值电阻R的阻值为6Ω，电动机的内阻为0.5Ω.求（取g=10m/s2,静电力常量k="9.0" ×109 N·m2/C2）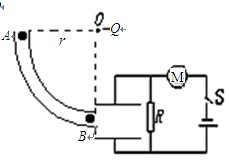
静止在光滑斜面底部的压缩弹簧的顶端此时小球距斜面顶端的高度为
.解除弹簧的锁定后,小球沿斜面向上运动.离开斜面后,达到最高点时(此时
发生弹性碰撞,碰撞后球
同一高度,球
上的
点, 
与
.已知球
,悬绳长
,视两球为质点,重力加速度为
,不计空气阻力.求:
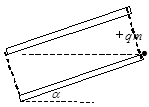
角的绝缘直杆
，其下端(
端)距地面高度
。有一质量
的带电小环套在直杆上，正以某一速度，沿杆匀速下滑，小环离杆后正好通过
点处。（
取
，
）
