题目内容
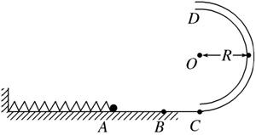
如图所示,在同一竖直平面上, 质量为2m的小球 静止在光滑斜面底部的压缩弹簧的顶端此时小球距斜面顶端的高度为
静止在光滑斜面底部的压缩弹簧的顶端此时小球距斜面顶端的高度为 .解除弹簧的锁定后,小球沿斜面向上运动.离开斜面后,达到最高点时(此时
.解除弹簧的锁定后,小球沿斜面向上运动.离开斜面后,达到最高点时(此时 球的速度恰好水平)与静止悬挂在此处的小球
球的速度恰好水平)与静止悬挂在此处的小球 发生弹性碰撞,碰撞后球
发生弹性碰撞,碰撞后球 刚好能摆到与悬点
刚好能摆到与悬点 同一高度,球
同一高度,球 沿水平方向抛射落在水平面
沿水平方向抛射落在水平面 上的
上的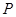 点,
点,  点的投影
点的投影 与
与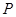 的距离为
的距离为 .已知球
.已知球 质量为
质量为 ,悬绳长
,悬绳长 ,视两球为质点,重力加速度为
,视两球为质点,重力加速度为 ,不计空气阻力.求:
,不计空气阻力.求:
(1)球 在两球碰撞后瞬间受到悬绳拉力的大小.
在两球碰撞后瞬间受到悬绳拉力的大小.
(2)球 在两球碰撞前瞬间的速度大小.
在两球碰撞前瞬间的速度大小.
(3)弹簧的弹力对球 所做的功.
所做的功.
(1)3mg(2) (3)
(3)
解析试题分析:⑴设球B在两球碰撞后一瞬间的速度大小为 ,则由动能定理
,则由动能定理 得
得 .
.
由牛顿第二定律 得
得
⑵设球A在两球碰撞前一瞬间的速度大小为 ,球A在两球碰撞后一瞬间的速度大小为
,球A在两球碰撞后一瞬间的速度大小为 ,
,
碰撞过程中满足动量守恒定律: ;
;
机械能守恒定律 
得 ,
,  .
.
⑶ 碰后球A做平抛运动,设碰后一瞬间球A距 的高度为
的高度为 :
: ,
,
得
弹簧将球A弹起到A碰B的过程中,由功能原理:
得 W弹= .
.
考点:此题考查了动能定理、牛顿定律、动量守恒定律及能量守恒定律。

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
 点,另一端系一质量
点,另一端系一质量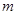 的小球,小球可视为质点。将轻绳拉至水平并将小球由位置A静止释放,小球运动到最低点时,轻绳刚好被拉断。
的小球,小球可视为质点。将轻绳拉至水平并将小球由位置A静止释放,小球运动到最低点时,轻绳刚好被拉断。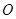 点为顶点的固定斜面,倾角
点为顶点的固定斜面,倾角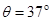 ,斜面足够长,且
,斜面足够长,且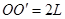 ,已知重力加速度为
,已知重力加速度为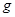 ,忽略空气阻力;求:
,忽略空气阻力;求: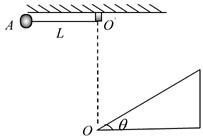
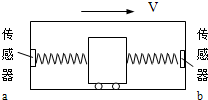
 =0.80m的轻绳一端固定在
=0.80m的轻绳一端固定在 点,另一端连接一质量
点,另一端连接一质量 距离水平地面的高度H = 1.00m。开始时小球处于
距离水平地面的高度H = 1.00m。开始时小球处于 点,此时轻绳拉直处于水平方向上,如图所示。让小球从静止释放,当小球运动到
点,此时轻绳拉直处于水平方向上,如图所示。让小球从静止释放,当小球运动到 正下方一个固定的钉子P时立刻断裂。不计轻绳断裂的能量损失,取重力加速度g=10m/s2。求:
正下方一个固定的钉子P时立刻断裂。不计轻绳断裂的能量损失,取重力加速度g=10m/s2。求: 
 点时的速度大小;
点时的速度大小; 点抛出并落在水平地面的C点,求C点与
点抛出并落在水平地面的C点,求C点与 点之间的水平距离;
点之间的水平距离;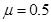 ,右侧BC段光滑。g=10m/s2,求:
,右侧BC段光滑。g=10m/s2,求: