题目内容
半径为R、质量为M的圆形薄板A与半径为r、质量为m的小球B用轻绳连接,开始时A与B挨在一起。在它们下方h=0.2m处有一固定支架C,支架中心有一半径为R’的圆孔(r<R’<R),圆孔、薄板和小球中心都在同一直线上,如图所示。现释放球与薄板,使它们一起自由下落,当薄板A落到固定支架C上时,与支架发生碰撞,碰撞时间极短,碰后薄板A以原速率返回,而球B继续向下运动,直到轻绳绷紧。绳的绷紧过程也极短,绷紧后球B与板A具有相同的速度v。

①若M=9m,轻绳的长度L满足什么条件,可使轻绳绷紧后的瞬间球与板的速率v的方向是向下的?
②若轻绳长度L=0.4m,M=km,试讨论绳绷紧后的瞬间,球与板的共同速度v的方向与k值的关系。
解析:
|
解 ①A与C相碰前,A.B一起作自由落体运动,末速度v0= A与C碰后以初速v0作竖直上抛运动,B继续向下运动,设这段运动经历时间t,显然 t≤ 则小球B自由下落的最大距离 sm=v0t+ 要使绳绷紧后的瞬间A.B的速度v方向向下,就要满足绳绷直前A.B的总动量方向向下,即 mv1+Mv2>0(M=9m), 设向下为正方向,绳刚绷直后的瞬间球的速度 v1= v0+gt,板的速度v2= - v0+ gt, 以板A为参考系,球B做速度为2 v0的匀速运动,时间 t=L/2 v0。 解以上各式,得L>0.64m,所以轻绳长度应满足的条件是0.64m<L≤0.8m。 ②当轻绳长0.4m时,由上面关系t=L/2 v0=0.1s, 绳临绷直时的速度v1=3m/s,v2= -1m/s, 绳绷直过程中,A.B系统动量守恒,m v1+M v2=(m+M)v, 可得v= |

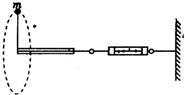 一宇航员抵达一半径为R的星球表面后,为了测定该星球的质量M,做如下实验,取一根细线穿过光滑的细直管,细线一端栓一质量为m的砝码,另一端连在一固定的测力计上,手握细直管抡动砝码,使它在竖直平面内做完整的圆周运动.停止抡动细直管,砝码可继续在同一竖直平面做完整的圆周运动.如图所示,观察测力计得到,当砝码运动到圆周的最低点时,测力计的读数为F1;当砝码运动到圆周的最高点时,测力计的读数为F2.已知引力常量为G,试根据题中提供的条件和测量结果,求:
一宇航员抵达一半径为R的星球表面后,为了测定该星球的质量M,做如下实验,取一根细线穿过光滑的细直管,细线一端栓一质量为m的砝码,另一端连在一固定的测力计上,手握细直管抡动砝码,使它在竖直平面内做完整的圆周运动.停止抡动细直管,砝码可继续在同一竖直平面做完整的圆周运动.如图所示,观察测力计得到,当砝码运动到圆周的最低点时,测力计的读数为F1;当砝码运动到圆周的最高点时,测力计的读数为F2.已知引力常量为G,试根据题中提供的条件和测量结果,求:

























 =
= 
















