题目内容
一个人以30m/s的初速度将小球上抛，每隔1s抛出一球．假设空气阻力可以忽略不计，而且升、降的球都不相碰(取
)，问：
(1)最多有几个小球在空中？
(2)设在t=0时将第1个小球抛出，在哪些时刻它和以后抛出的小球在空中相遇而过？
答案：略
解析：
解析：
|
小球都做竖直上抛运动，求出每个小球在空中运动的时间，就知道空中最多能有几个小球．欲求相遇时刻，可根据相遇时小球的位移相等来求解． (1) 小球做竖直上抛运动在空中经历的时间为
当 t=0时，将第1个小球抛出后，它于第6s末回到原处；同时第7个小球即将抛出．在第6个小球抛出后，第1个小球尚未返回到地面，空中共有6个小球；第7个小球抛出时，第1个小球已落地，所以空中最多只有6个小球．(2) 第1个小球于t=0时抛出，而第n个小球于Δt后抛出，NU在某一时刻t，这两个小球的位移分别为
两个小球在空中相遇时它们的位移相等，即
则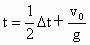 
上式中 t表示第1个小球和Δt时间后抛出的小球在空中相遇而过的时刻，由题给条件：当 Δt=s时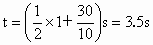， ，这是第1个小球和第2个小球相遇而过的时刻．
当 Δt=2s时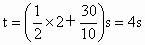， ，这是第1个小球和第3个小球相遇而过的时刻．
当 Δt=3s时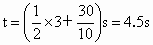， ，这是第1个小球和第4个小球相遇而过的时刻．
当 Δt=4s时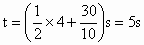， ，这是第1个小球和第5个小球相遇而过的时刻．
当 Δt=5s时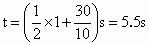， ，这是第1个小球和第6个小球相遇而过的时刻． |
练习册系列答案
灵星计算小达人系列答案
相关题目
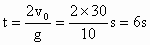
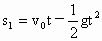
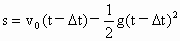
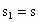
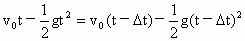
)，问：