题目内容
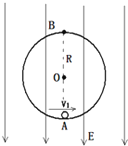
【题目】如图,内表面光滑绝缘的半径为![]() 的圆形轨道处于竖直平面内,有竖直向下的匀强电场,场强大小为
的圆形轨道处于竖直平面内,有竖直向下的匀强电场,场强大小为![]() 有一质量为
有一质量为![]() 、带负电的小球,电量
、带负电的小球,电量![]() ,小球在圆轨道内壁做圆周运动,当运动到最低点A时,小球与轨道压力恰好为零,g取
,小球在圆轨道内壁做圆周运动,当运动到最低点A时,小球与轨道压力恰好为零,g取![]() ,空气阻力不计,求:
,空气阻力不计,求:
![]() 小球在A点处的速度大小.
小球在A点处的速度大小.
![]() 小球运动到最高点B时对轨道的压力.
小球运动到最高点B时对轨道的压力.
![]() 若当小球运动到A点时,立即将电场方向改为水平向右,并给小球补充一定的动能。补充后小球恰好可以在圆轨道内壁做完整的圆周运动,则应该补充的动能是多少?若取过A点的水平面为重力势能零势面,则小球运动过程中的机械能的最大值是多少?
若当小球运动到A点时,立即将电场方向改为水平向右,并给小球补充一定的动能。补充后小球恰好可以在圆轨道内壁做完整的圆周运动,则应该补充的动能是多少?若取过A点的水平面为重力势能零势面,则小球运动过程中的机械能的最大值是多少?
【答案】![]() ;
;![]() ;
;![]() 应该补充的动能是
应该补充的动能是![]() ;若取过A点的水平面为重力势能零势面,则小球运动过程中的机械能的最大值是
;若取过A点的水平面为重力势能零势面,则小球运动过程中的机械能的最大值是![]() 。
。
【解析】
(1)重力:![]() ,
,
电场力:![]() ,
,
在A点,有:![]() ,
,
代入数据解得:![]() ;
;
(2)设球在B点的速度大小为![]() ,从A到B,由动能定理有:
,从A到B,由动能定理有:
![]() ,
,
在B点,设轨道对小球弹力为![]() ,则有:
,则有:![]() ,
,
由牛顿第三定律有:![]() ,
,
代入数据解得:![]() ;
;
(3)电场方向改变后,重力和电场力的合力大小![]() ,
,
解得![]() ,
,
方向左偏下与水平方向成,且![]() ,
,
故其运动到O点右上方与水平方向的夹角为的C点时,其速度有最小值![]() ,令小球补充能量后的速度大小为v,则其从A到C的过程中,由动能定理可得:
,令小球补充能量后的速度大小为v,则其从A到C的过程中,由动能定理可得:![]() ,
,
在C点,有![]() ,补充能量为
,补充能量为![]() ,
,
解得![]() ,
,
由能量守恒可知,当电势能最小时,机械能最大,
故当其运动到O点正左方时,机械能有最大值,![]()
解得![]() 。
。

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目