Question

沿半径为R的半球型碗底的光滑内表面，质量为m的小球正以角速度ω，在一水平面内作匀速圆周运动，试求此时小球离碗底的高度h．

Answer 1

分析：小球在光滑碗内靠重力和支持力的合力提供向心力，根据向心力和重力的关系求出小球与半球形碗球心连线与竖直方向的夹角，根据几何关系求出平面离碗底的距离h．

解答：解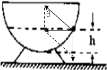：小球靠重力和支持力的合力提供向心力，小球做圆周运动的半径为r=Rsinθ，
根据力图可知tanθ=

F向

mg

=

mRsinθω2

mg

；
解得cosθ=

g

Rω2

．
所以h=R-Rcosθ=R-

g

ω2

．
答：此时小球离碗底的高度h为R-

g

ω2

．

点评：解决本题的关键知道小球做圆周运动向心力的来源，运用牛顿第二定律和几何关系进行求解．