Question

如图所示，-个质量为m的人站在台秤上，跨过光滑定滑轮将质量为m′的重物从高处放下，设重物以加速度a加速下降（a＜g），且m′＜m，则台秤上的示数为（ ）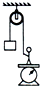

A．（m+m′）g-m′a
B．（m-m′）g+m′a
C．（m-m′）g-m′a
D．（m-m′）g

Answer 1

【答案】分析：先对重物受力分析，受重力和拉力，加速下降，然后根据牛顿第二定律列式求出绳子的拉力；再对人受力分析，受到重力、拉力和支持力，根据平衡条件求出支持力，而台秤读数等于支持力．
解答：解：对重物受力分析，受重力和拉力，加速下降，根据牛顿第二定律，有：m′g-T=m′a      ①
再对人受力分析，受到重力、拉力和支持力，根据共点力平衡条件，有：N+T=mg          ②
由①②，解得
N=（m-m′）g+m′a
故选B．
点评：本题关键是分别对重物和人受力分析，然后根据牛顿第二定律和平衡条件列式求解．