题目内容
 如图甲所示,长为a宽为b,单位长度电阻为r的均匀线框从磁感应强度为B的匀强磁场中以速度V匀速拉出,求拉力的功及PQ两点间的电势差.如果线框以图乙方式匀速拉出,为使外力的功与图甲方式相同,拉出的速度V1应为多大?此时PQ两点间的电势差多大?
如图甲所示,长为a宽为b,单位长度电阻为r的均匀线框从磁感应强度为B的匀强磁场中以速度V匀速拉出,求拉力的功及PQ两点间的电势差.如果线框以图乙方式匀速拉出,为使外力的功与图甲方式相同,拉出的速度V1应为多大?此时PQ两点间的电势差多大?分析:根据法拉第电磁感应、欧姆定律求出感应电流,由公式F=BIL求出安培力的大小.线框匀速运动,拉力与安培力大小相等,求得拉力,即可求得做功.根据欧姆定律求PQ两点间的电势差.
再用同样的方法求速度V1及PQ两点间的电势差.
再用同样的方法求速度V1及PQ两点间的电势差.
解答:解:(1)线框以速度V匀速拉出时,产生的感应电动势为:E=Bbv
感应电流为:I=
=
线框所受安培力大小为:F安=BIb=
,
因线框匀速运动,则拉力为:F拉=F安.
故拉力的功为:W=F拉a=
a.PQ两点间的电势差为:UPQ=Iar=
ar=
(2)如果线框以图乙方式匀速拉出,同理可得,拉力的功为:W′=
为使外力的功与图甲方式相同,则有:
a=
得:v1=
感应电流为:I′=
=
PQ两点间的电势差为:UPQ′=I′ar=
ar=
答:拉力的功是
a.PQ两点间的电势差是
.如果线框以图乙方式匀速拉出,为使外力的功与图甲方式相同,拉出的速度V1应为
.此时PQ两点间的电势差是
.
感应电流为:I=
| E |
| R |
| Bbv |
| 2(a+b)r |
线框所受安培力大小为:F安=BIb=
| B2b2v |
| 2(a+b)r |
因线框匀速运动,则拉力为:F拉=F安.
故拉力的功为:W=F拉a=
| B2b2v |
| 2(a+b)r |
| Bbv |
| 2(a+b)r |
| Bbav |
| 2(a+b) |
(2)如果线框以图乙方式匀速拉出,同理可得,拉力的功为:W′=
| B2a2bv1 |
| 2(a+b)r |
为使外力的功与图甲方式相同,则有:
| B2b2v |
| 2(a+b)r |
| B2a2bv1 |
| 2(a+b)r |
得:v1=
| bv |
| a |
感应电流为:I′=
| Bav1 |
| 2(a+b)r |
| Bbv |
| 2(a+b)r |
PQ两点间的电势差为:UPQ′=I′ar=
| Bbv |
| 2(a+b)r |
| Babv |
| 2(a+b) |
答:拉力的功是
| B2b2v |
| 2(a+b)r |
| Bbav |
| 2(a+b) |
| bv |
| a |
| Babv |
| 2(a+b) |
点评:本题是电磁感应与电路的综合,关键求解安培力,根据欧姆定律分析PQ间的电压.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
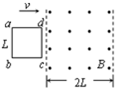 如图甲所示,空间有一宽为2L的匀强磁场区域,磁感应强度为B,方向垂直纸面向外.abcd是由均匀电阻丝做成的边长为L的正方形线框,总电阻为R.线框以垂直磁场边界的速度v匀速通过磁场区域.在运动过程中,线框ab、cd两边始终与磁场边界平行.设线框刚进入磁场的位置x=0,x轴沿水平方向向右.则ab两端电势差Uab随距离变化的图象正确的是(其中U0=BLv)( )
如图甲所示,空间有一宽为2L的匀强磁场区域,磁感应强度为B,方向垂直纸面向外.abcd是由均匀电阻丝做成的边长为L的正方形线框,总电阻为R.线框以垂直磁场边界的速度v匀速通过磁场区域.在运动过程中,线框ab、cd两边始终与磁场边界平行.设线框刚进入磁场的位置x=0,x轴沿水平方向向右.则ab两端电势差Uab随距离变化的图象正确的是(其中U0=BLv)( ) (2012?嘉兴二模)某兴趣小组欲通过测定工业污水(含多种重金属离子)的电阻率来判断某工厂废水是否达到排放标准(一般工业废水电阻率的达标值为ρ≥200Ω?m).如图甲所示为该同学所用盛水容器,其左、右两侧面为金属薄板(电阻极小),其余四面由绝缘材料制成,左右两侧带有接线柱.容器内表面长a=40cm,宽b=20cm,高c=10cm.将水样注满容器后,进行以下操作:
(2012?嘉兴二模)某兴趣小组欲通过测定工业污水(含多种重金属离子)的电阻率来判断某工厂废水是否达到排放标准(一般工业废水电阻率的达标值为ρ≥200Ω?m).如图甲所示为该同学所用盛水容器,其左、右两侧面为金属薄板(电阻极小),其余四面由绝缘材料制成,左右两侧带有接线柱.容器内表面长a=40cm,宽b=20cm,高c=10cm.将水样注满容器后,进行以下操作: 水样的电阻约为
水样的电阻约为 (3)正确连接电路后,闭合开关,测得一组U、I数据;再调节滑动变阻器,重复上述测量步骤,得出一系列数据如表所示,请在在答题卷相应位置的坐标纸中作出U-I关系图线.
(3)正确连接电路后,闭合开关,测得一组U、I数据;再调节滑动变阻器,重复上述测量步骤,得出一系列数据如表所示,请在在答题卷相应位置的坐标纸中作出U-I关系图线.




