题目内容
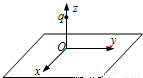 如图所示,xOy平面是无穷大导体的表面,该导体充满z<0的空间,z>0的空间为真空.将电荷为q的点电荷置于z轴上z=h处,则在xOy平面上会产生感应电荷.空间任意一点处的电场皆是由点电荷q和导体表面上的感应电荷共同激发的.已知静电平衡时导体内部场强处处为零,则在z轴上z=h/2处的场强大小为(k为静电力常量)( )
如图所示,xOy平面是无穷大导体的表面,该导体充满z<0的空间,z>0的空间为真空.将电荷为q的点电荷置于z轴上z=h处,则在xOy平面上会产生感应电荷.空间任意一点处的电场皆是由点电荷q和导体表面上的感应电荷共同激发的.已知静电平衡时导体内部场强处处为零,则在z轴上z=h/2处的场强大小为(k为静电力常量)( )A.
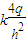
B.
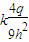
C.
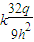
D.
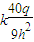
【答案】分析:根据对称性,感应电荷在导体内外两侧空间产生的电场强度的大小相等,方向相反;而内部一点的电场强度为q和感应电荷产生的电场强度的合矢量.
解答:解:在z轴上-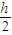 处,合场强为零,该点场强为q和导体近端感应电荷产生电场的场强的矢量和;
处,合场强为零,该点场强为q和导体近端感应电荷产生电场的场强的矢量和;
q在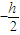 处产生的场强为:
处产生的场强为: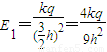 ;
;
由于导体远端离-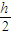 处很远,影响可以忽略不计,故导体在-
处很远,影响可以忽略不计,故导体在-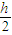 处产生场强近似等于近端在-
处产生场强近似等于近端在-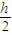 处产生的场强;
处产生的场强;
-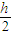 处场强为:0=E1+E2,故
处场强为:0=E1+E2,故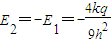 ;
;
根据对称性,导体近端在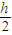 处产生的场强为
处产生的场强为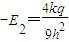 ;
;
电荷q在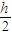 处产生的场强为:
处产生的场强为: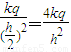 ;
;
故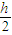 处的合场强为:
处的合场强为: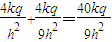 ;
;
故选D.
点评:本题考查了导体的静电平衡和场强的叠加原理,要结合对称性进行近似运算,难题.
解答:解:在z轴上-
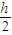 处,合场强为零,该点场强为q和导体近端感应电荷产生电场的场强的矢量和;
处,合场强为零,该点场强为q和导体近端感应电荷产生电场的场强的矢量和;q在
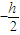 处产生的场强为:
处产生的场强为: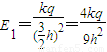 ;
;由于导体远端离-
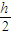 处很远,影响可以忽略不计,故导体在-
处很远,影响可以忽略不计,故导体在-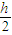 处产生场强近似等于近端在-
处产生场强近似等于近端在-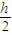 处产生的场强;
处产生的场强;-
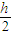 处场强为:0=E1+E2,故
处场强为:0=E1+E2,故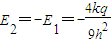 ;
;根据对称性,导体近端在
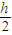 处产生的场强为
处产生的场强为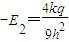 ;
;电荷q在
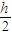 处产生的场强为:
处产生的场强为: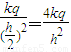 ;
;故
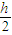 处的合场强为:
处的合场强为: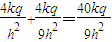 ;
;故选D.
点评:本题考查了导体的静电平衡和场强的叠加原理,要结合对称性进行近似运算,难题.

练习册系列答案
相关题目
 (2010?云南模拟)如图所示,xOy平面内,第二象限匀强电场方向水平向右,第一象限匀强电场方向竖直向下,场强大小相等,设为E.x轴下方区域有垂直于纸面向外的匀强磁场,磁感应强度设为B,图中OP直线与纵轴的夹角α=45°,一带正电的粒子从OP直线上某点A(-L,L)处由静止释放,重力不计.设粒子质量为m,带电量为q,E、B、m、q均未知,但已知各量都使用国际制单位时,从数值上有B=
(2010?云南模拟)如图所示,xOy平面内,第二象限匀强电场方向水平向右,第一象限匀强电场方向竖直向下,场强大小相等,设为E.x轴下方区域有垂直于纸面向外的匀强磁场,磁感应强度设为B,图中OP直线与纵轴的夹角α=45°,一带正电的粒子从OP直线上某点A(-L,L)处由静止释放,重力不计.设粒子质量为m,带电量为q,E、B、m、q均未知,但已知各量都使用国际制单位时,从数值上有B= 如图所示的xoy平面区域内存在电场,一个正电荷先后两次从C点分别沿直线被移动到A点和B点,在这两个过程中,均需克服电场力做功,且做功的数值相等.那么这一区域内的电场可能是( )
如图所示的xoy平面区域内存在电场,一个正电荷先后两次从C点分别沿直线被移动到A点和B点,在这两个过程中,均需克服电场力做功,且做功的数值相等.那么这一区域内的电场可能是( ) 如图所示的xOy平面内有一半径为R、以坐标原点O为圆心的圆形磁场区域,磁场方向垂直纸面向外,在直线x=R和x=R+L之间有向y轴负方向的匀强电场,在原点O处有一离子源向y轴正方向发射速率为v0的带电离子,离子射出磁场一段时间后进入电场,最终从x轴上的P(R+L,0)点射出电场,不计离子重力,求电场强度E与磁感应强度B的比值.
如图所示的xOy平面内有一半径为R、以坐标原点O为圆心的圆形磁场区域,磁场方向垂直纸面向外,在直线x=R和x=R+L之间有向y轴负方向的匀强电场,在原点O处有一离子源向y轴正方向发射速率为v0的带电离子,离子射出磁场一段时间后进入电场,最终从x轴上的P(R+L,0)点射出电场,不计离子重力,求电场强度E与磁感应强度B的比值. 如图所示为xOy平面内沿x轴传播的简谐横波在t=0时刻的波形图象,波速为1cm/s,此时P点沿+y轴方向运动,则下列说法正确的是( )
如图所示为xOy平面内沿x轴传播的简谐横波在t=0时刻的波形图象,波速为1cm/s,此时P点沿+y轴方向运动,则下列说法正确的是( )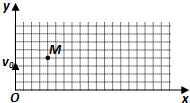 在如图所示的xoy平面内(y轴的正方向竖直向上)存在着水平向右的匀强电场,有带正电的小球自坐标原点O沿y轴的正方向竖直向上抛出,它的初动能为5J,不计空气阻力,当它上升到最高点M时,动能为4J.
在如图所示的xoy平面内(y轴的正方向竖直向上)存在着水平向右的匀强电场,有带正电的小球自坐标原点O沿y轴的正方向竖直向上抛出,它的初动能为5J,不计空气阻力,当它上升到最高点M时,动能为4J.