题目内容
 如图所示的xOy平面内有一半径为R、以坐标原点O为圆心的圆形磁场区域,磁场方向垂直纸面向外,在直线x=R和x=R+L之间有向y轴负方向的匀强电场,在原点O处有一离子源向y轴正方向发射速率为v0的带电离子,离子射出磁场一段时间后进入电场,最终从x轴上的P(R+L,0)点射出电场,不计离子重力,求电场强度E与磁感应强度B的比值.
如图所示的xOy平面内有一半径为R、以坐标原点O为圆心的圆形磁场区域,磁场方向垂直纸面向外,在直线x=R和x=R+L之间有向y轴负方向的匀强电场,在原点O处有一离子源向y轴正方向发射速率为v0的带电离子,离子射出磁场一段时间后进入电场,最终从x轴上的P(R+L,0)点射出电场,不计离子重力,求电场强度E与磁感应强度B的比值.分析:根据离子在磁场中做匀速圆周运动,然后做匀速直线运动,最后在电场中做类平抛运动,并根据左手定则,可确定离子的带电性质.根据类平抛运动和几何关系计算离子的比荷与场强E的关系式.
离子在磁场中做圆周运动,洛伦兹力提供离子做圆周运动的向心力,列式即可求解电场强度E与磁感应强度B的比值.
离子在磁场中做圆周运动,洛伦兹力提供离子做圆周运动的向心力,列式即可求解电场强度E与磁感应强度B的比值.
解答:解:离子源向y轴正方向发射速率v0的带电离子,离子射出磁场时速度与x轴平行,则受的洛伦兹力水平向右,根据左手定则,磁场从掌心穿入,拇指指向洛伦兹力的方向,四指指向正电荷运动的方向,所以该离子带正电.
离子运动轨迹如图所示,设离子在磁场中做圆周运动的半径为r,据几何关系可得:r=
R.①
粒子在电场中做类平抛运动
x正方向上做匀速直线运动,位移为 L=v0t,②
y负方向上做初速度为零的匀加速运动,位移为 r=
at2,③
根据牛顿第二定律,粒子的加速度为 a=
④
所以联立以上各式得:
=
;⑤
离子在磁场中做圆周运动,洛伦兹力提供离子做圆周运动的向心力,则得:
qv0B=m
⑥
由①⑤⑥解得,
=
答:电场强度E与磁感应强度B的比值为
.

离子运动轨迹如图所示,设离子在磁场中做圆周运动的半径为r,据几何关系可得:r=
| ||
| 2 |
粒子在电场中做类平抛运动
x正方向上做匀速直线运动,位移为 L=v0t,②
y负方向上做初速度为零的匀加速运动,位移为 r=
| 1 |
| 2 |
根据牛顿第二定律,粒子的加速度为 a=
| qE |
| m |
所以联立以上各式得:
| q |
| m |
| ||||
| EL2 |
离子在磁场中做圆周运动,洛伦兹力提供离子做圆周运动的向心力,则得:
qv0B=m
| ||
| r |
由①⑤⑥解得,
| E |
| B |
| v0R2 |
| L2 |
答:电场强度E与磁感应强度B的比值为
| v0R2 |
| L2 |
点评:本题关键运用牛顿第二定律与运动学公式,处理带电粒子在组成场中运动的问题,掌握几何关系的运用,并学会正确画出运动轨迹.

练习册系列答案
相关题目
 如图所示的xoy平面区域内存在电场,一个正电荷先后两次从C点分别沿直线被移动到A点和B点,在这两个过程中,均需克服电场力做功,且做功的数值相等.那么这一区域内的电场可能是( )
如图所示的xoy平面区域内存在电场,一个正电荷先后两次从C点分别沿直线被移动到A点和B点,在这两个过程中,均需克服电场力做功,且做功的数值相等.那么这一区域内的电场可能是( ) (2013?琼海模拟)如图所示的xoy平面内有一半径为R、以坐标原点o为圆心的圆形磁场区域,磁场方向垂直纸面向外,在直线x=R和x=R+L之间有向y轴负方向的匀强电场,在原点o有一离子源向y轴正方向发射速率v0的带电离子,离子射出磁场时速度与x轴平行,射出磁场一段时间后进入电场,电场强度为E,最终从x轴上的P(R+L,0)点射出电场,不计离子重力,求:
(2013?琼海模拟)如图所示的xoy平面内有一半径为R、以坐标原点o为圆心的圆形磁场区域,磁场方向垂直纸面向外,在直线x=R和x=R+L之间有向y轴负方向的匀强电场,在原点o有一离子源向y轴正方向发射速率v0的带电离子,离子射出磁场时速度与x轴平行,射出磁场一段时间后进入电场,电场强度为E,最终从x轴上的P(R+L,0)点射出电场,不计离子重力,求: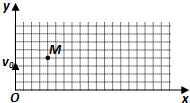 在如图所示的xoy平面内(y轴的正方向竖直向上)存在着水平向右的匀强电场,有带正电的小球自坐标原点O沿y轴的正方向竖直向上抛出,它的初动能为5J,不计空气阻力,当它上升到最高点M时,动能为4J.
在如图所示的xoy平面内(y轴的正方向竖直向上)存在着水平向右的匀强电场,有带正电的小球自坐标原点O沿y轴的正方向竖直向上抛出,它的初动能为5J,不计空气阻力,当它上升到最高点M时,动能为4J. 和
和 之间有向y轴负方向的匀强电场,在原点O有一离子源向y轴正方向发射速率为v0的带电离子,离子射出磁场时速度与x轴平行,射出磁场一段时间后进入电场,最终从x轴上的P(R+L,0)点射出电场,不计离子重力,求电场强度E与磁感应强度B的比值。
之间有向y轴负方向的匀强电场,在原点O有一离子源向y轴正方向发射速率为v0的带电离子,离子射出磁场时速度与x轴平行,射出磁场一段时间后进入电场,最终从x轴上的P(R+L,0)点射出电场,不计离子重力,求电场强度E与磁感应强度B的比值。