题目内容
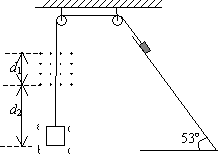
如图，一边长L＝0.4 m、质量m1＝0.2 kg、电阻R＝0.1 
的正方形导体线框abcd，与一质量为m2＝1.0 kg的物块通过轻质细线跨过两定滑轮相连．磁感应强度B＝1.0 T，磁场宽度d1＝0.8 m，开始时bc边距磁场下边界为d2＝1.0 m，物块放在倾角θ＝53o的斜面上，物块与斜面间的动摩擦因数为m
＝
．现将物块由静止释放，经过一段时间后发现当ad边从磁场上边缘穿出时，线框恰好做匀速运动，已知sin53o＝0.8，cos53o＝0.6取g＝10 m/s2．求：
(1)线框ad边从磁场上边缘穿出时速度的大小；
(2)线框ad边刚刚进入磁场时的动能；
(3)线框从开始运动到全部穿出磁场的过程中产生的焦耳热．
答案：
解析：
解析：
(1)设速度为v1，物块此后也匀速运动
对m2：T＋m m2gcos53o－m2gsin53o＝0(1分) 求得：T＝6 N(1分)
对m1：T－m1g－F安＝0(1分) F安＝BIL(1分)
I＝＝(1分) 可求得：v1＝2.5 m/s(1分)
(2)设线框ad边刚刚进入磁场时，速度为v2，对整体有
(m2gsin53o－m m2gcos53o)(d2－L)－m1g(d2－L)＝(m1＋m2)v22(3分)
解得 v2＝2 m/s 故Ek＝m1v12＝0.4 J(1分)
(3)从开始运动到bc边离开磁场，对整体有
(m2gsin53o－m m2gcos53o)(d1＋d2)－m1g(d1＋d2)－W安＝(m1＋m2)v12(2分)
对线框有Q＝W安(1分) 解得：Q＝3.45 J(1分)
练习册系列答案
百年学典课时学练测系列答案
仁爱英语同步练习册系列答案
相关题目
（3）整个运动过程中线框产生的焦耳热。
，sin53°＝0.8，cos53°＝0.6）求： 
，sin53°＝0.8，cos53°＝0.6）求： 
的正方形导体线框abcd，与一质量为m2＝1.0kg的物块通过轻质细线跨过两定滑轮相连。磁感应强度B＝1.0T，磁场宽度d1＝0.8m，开始时bc边距磁场下边界为d2＝1.0m，物块放在倾角θ＝53º的斜面上，物块与斜面间的动摩擦因数为m＝。现将物块由静止释放，经过一段时间后发现当ad边从磁场上边缘穿出时，线框恰好做匀速运动，已知sin53º＝0.8，cos53º＝0.6取g＝10m/s2。求：