题目内容
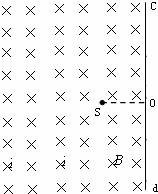 如图,真空室内存在一有右边界的匀强磁场区域,磁感应强度B=0.332T,磁场方向垂直于纸面向里,右边界cd为荧光屏(粒子打上去会发光).在磁场中距荧光屏d=8cm处有一点状α粒子放射源S,可沿纸面向各个方向均匀放射初速率相同的α粒子,已知:α粒子的质量m=6.64×10-27kg,电荷量q=3.2×10-19C,初速度v=3.2×106m/s.(可能用到的三角函数:sin37°=0.6,sin30°=0.5)求:
如图,真空室内存在一有右边界的匀强磁场区域,磁感应强度B=0.332T,磁场方向垂直于纸面向里,右边界cd为荧光屏(粒子打上去会发光).在磁场中距荧光屏d=8cm处有一点状α粒子放射源S,可沿纸面向各个方向均匀放射初速率相同的α粒子,已知:α粒子的质量m=6.64×10-27kg,电荷量q=3.2×10-19C,初速度v=3.2×106m/s.(可能用到的三角函数:sin37°=0.6,sin30°=0.5)求:(1)α粒子在磁场中作圆周运动的轨道半径R;
(2)荧光屏cd被α粒子射中而发光的区域长度L;
(3)若从放射源打出的α粒子总个数为3.6×1010个,则最终能打到荧光屏上的α粒子个数为多少?
分析:(1)根据洛伦兹力提供向心力,求出带电粒子在磁场中的轨道半径公式,从而求出半径的大小.
(2)放射源S可沿纸面向各个方向均匀放射初速率相同的α粒子,根据几何关系,粒子打在O点上方的最高点时,轨迹与光屏相切.在O点下方的最低点与放射源的连线等于直径,结合半径的大小结合几何关系求出发光的区域长度L.
(3)根据几何关系找出不能打在光屏上的粒子速度方向的范围,从而得出能够打在光屏上粒子的角度范围,从而确定出最终能打到荧光屏上的α粒子个数.
(2)放射源S可沿纸面向各个方向均匀放射初速率相同的α粒子,根据几何关系,粒子打在O点上方的最高点时,轨迹与光屏相切.在O点下方的最低点与放射源的连线等于直径,结合半径的大小结合几何关系求出发光的区域长度L.
(3)根据几何关系找出不能打在光屏上的粒子速度方向的范围,从而得出能够打在光屏上粒子的角度范围,从而确定出最终能打到荧光屏上的α粒子个数.
解答:解:(1)由qvB=m
得,R=
=
=0.2m=20cm 
(2)粒子打在O点上方的最高点时,轨迹与光屏相切.在O点下方的最低点与放射源的连线等于直径,轨迹如图.
O点上方最高点与O点的距离y1=
=16cm.
O点下方最低点与O点的距离y2=
=16
cm.
发光长度为:L=16(1+
)cm.
(3)粒子能打在荧光屏上的速度方向介于如下图所示的两个速度之间,根据几何关系得,θ=360°-(180°-2×37°)=254°
则最终能打到荧光屏上的α粒子个数为n=
×3.6×1010=2.54×1010.

答:(1)α粒子在磁场中作圆周运动的轨道半径R为0.2m.
(2)荧光屏cd被α粒子射中而发光的区域长度L=16(1+
)cm.
(3)最终能打到荧光屏上的α粒子个数为2.54×1010个.
| v2 |
| R |
| mv |
| qB |
| 6.64×10-27×3.2×106 |
| 3.2×10-19×0.332 |

(2)粒子打在O点上方的最高点时,轨迹与光屏相切.在O点下方的最低点与放射源的连线等于直径,轨迹如图.
O点上方最高点与O点的距离y1=
| 202-(20-8)2 |
O点下方最低点与O点的距离y2=
| 402-82 |
| 6 |
发光长度为:L=16(1+
| 6 |
(3)粒子能打在荧光屏上的速度方向介于如下图所示的两个速度之间,根据几何关系得,θ=360°-(180°-2×37°)=254°
则最终能打到荧光屏上的α粒子个数为n=
| 254 |
| 360 |

答:(1)α粒子在磁场中作圆周运动的轨道半径R为0.2m.
(2)荧光屏cd被α粒子射中而发光的区域长度L=16(1+
| 6 |
(3)最终能打到荧光屏上的α粒子个数为2.54×1010个.
点评:解决本题的关键确定带电粒子运动轨迹的临界状态,本题涉及两个临界状态,题目中第二问涉及的是粒子能够打在光屏上的范围这种临界,第三问涉及的是粒子能够打在光屏上的临界.对数学几何能力的要求较高.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
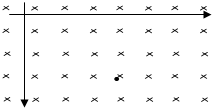 如图,真空室内存在匀强磁场,磁场方向垂直于纸面向里,磁感应强度的大小B=0.6T,在磁场内建立一直角坐标系,坐标系平面与磁场垂直.坐标系平面内的P点距x、y轴的距离分别为16cm和18cm.P处有一个点状的α放射源,它向各个方向发射α粒子,α粒子的速度都是v=3.0×106m/s,已知α粒子的电荷与质量之比
如图,真空室内存在匀强磁场,磁场方向垂直于纸面向里,磁感应强度的大小B=0.6T,在磁场内建立一直角坐标系,坐标系平面与磁场垂直.坐标系平面内的P点距x、y轴的距离分别为16cm和18cm.P处有一个点状的α放射源,它向各个方向发射α粒子,α粒子的速度都是v=3.0×106m/s,已知α粒子的电荷与质量之比
 放射源,它向各个方向发射
放射源,它向各个方向发射 ,已知
,已知 ,现只考虑在坐标系平面中运动的
,现只考虑在坐标系平面中运动的
