Question

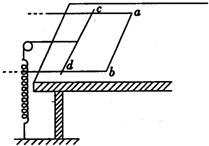（2013?河南模拟）如图所示，在一光滑水平的桌面上，放置一质量为M，宽为L的足够长“U”型框架，其ab部分电阻为R，框架其它部分的电阻不计．垂直框架两边放一质量为m、电阻为R的金属棒cd，它们之间的动摩擦因数为μ，棒通过细线跨过一定滑轮与劲度系数为k的另一端固定的轻弹簧相连．开始弹簧处于自然状态，框架和棒均静止．现在让框架在大小为2μmg的水平拉力作用下，向右做加速运动，引起棒的运动可看成是缓慢的．水平桌面位于竖直向上的匀强磁场中，磁感应强度为B．问：
（1）框架和棒刚开始运动的瞬间，框架的加速度为多大？
（2）框架最后做匀速运动（棒处于静止状态）时的速度多大？
（3）若框架通过位移S 后开始匀速，已知弹簧的弹性势能的表达式为

1

2

 kx²（x为弹簧的形变量），则在框架通过位移 s 的过程中，回路中产生的电热为多少？

Answer 1

分析：（1）对框架分析，运用牛顿第二定律求出框架的加速度．
（2）当框架所受合力为零时，框架做匀速运动，根据平衡，结合切割产生的感应电动势公式、闭合电路欧姆定律和安培力公式求出稳定时速度大小．
（3）根据功能关系以及框架和棒子都平衡求出回路产生的电热．

解答：解：（1）设水平拉力为F，则F=2μmg，对框架由牛顿第二定律：F-μmg=Ma，
解出a=

μmg

M

．
（2）设框架做匀速运动的速度大小为v，则感应电动势  E=BLv，回路中的电流 I=

E

R+R

，
对框架由力的平衡得F=BIL+μmg，联立以上各式解出 v=

2Rμmg

B2L2

（3）在框架滑过S的过程中，设产生的电热为Q_l，摩擦生热为Q₂，
由功能关系Fs=

1

2

Kx2+

1

2

Mv2+Q1+Q2，其中Q₂=μmg（S-x），
在框架匀速后，对棒由力的平衡得 BIL+μmg=Kx，
联立以上各式并结合F=BIL+μmg，F=2μmg，解出 Q1=μmgS-

2MR2μ2m2g2

B4L4

．
答：（1）框架和棒刚开始运动的瞬间，框架的加速度为a=

μmg

M

；   
（2）框架最后做匀速运动（棒处于静止状态）时的速度v=

2Rμmg

B2L2

； 
（3）回路中产生的电热Q1=μmgS-

2MR2μ2m2g2

B4L4

．

点评：本题是一条学科内综合题，同时又是一条新情景试题，本题物理过程较复杂，涉及弹性力、磁场力、摩擦力、牛顿第二定律、感应电动势、全电路欧姆定律、功能关系、力的平衡等众多知识点，考查考生多角度探究问题的能力．
解题关键：理清物理过程，分析各个物理过程中的受力时，不要漏掉力； 正确把握各个物理量的关系，在各个过程中选用合适的规律求解．，特别要关注各个力所对应的能量．