题目内容
17. 如图,A、B分别是光滑斜面的顶端和底端,F是斜面上的一个点,E点在F点的正上方,从E点以一定的水平速度抛出一个弹性小球,小球与斜面之间的碰撞无能量损失,其中EF间的高度为H,斜面的倾角为α=60°,重力加速度为g,斜面足够长,不计空气阳力.(计算结果可以用根式表示)
如图,A、B分别是光滑斜面的顶端和底端,F是斜面上的一个点,E点在F点的正上方,从E点以一定的水平速度抛出一个弹性小球,小球与斜面之间的碰撞无能量损失,其中EF间的高度为H,斜面的倾角为α=60°,重力加速度为g,斜面足够长,不计空气阳力.(计算结果可以用根式表示)(1)如果小球正好垂直打在斜面上,求小球在碰撞之前在空中飞行的时间为多少?
(2)如果小球与斜面碰撞后,恰好水平飞出,求小球第1次碰撞时速度的大小;
(3)如果小球与斜面碰撞后,恰好水平飞出,求小球从第1次与斜面碰撞到第n次碰撞时,小球的位移是多少?
分析 (1)小球做平抛运动,正好垂直打在斜面上时速度与斜面垂直.根据几何关系分析小球打在斜面上时分速度的关系,由平抛分位移公式求小球在碰撞之前在空中飞行的时间.
(2)根据对称性可知,小球落在斜面上时的速度方向与水平方向成α角.再用同样的方法求出时间,再由分速度公式和速度合成求小球第1次碰撞时速度.
(3)小球从第1次与斜面碰撞后,把此运动分解为平行于斜面与垂直于斜面两个方向.垂直于斜面方向建立y轴:小球先正向匀减速到0,然后返回与斜面相碰,以后重复,周期性往复运动,且运动周期为 T=$\frac{2v′sinα}{gcosα}$.沿斜面向下建立x轴,在x轴上小球做初速度为v′cosα、加速度为 gsinα的匀加速直线运动.根据周期性和位移公式求解位移.
解答 解:(1)小球正好垂直打在斜面上,根据平抛运动的规律有
水平方向:x=v0t
竖直方向:h1=$\frac{{v}_{y}}{2}t$
由几何关系得 $\frac{{v}_{0}}{{v}_{y}}$=tan60°
联立以上三式解得 x=2$\sqrt{3}$h1
则 h2=xtan60°=6h1
而 H=h1+h2,
可得 h1=$\frac{H}{7}$
由 h1=$\frac{1}{2}g{t}^{2}$,得 t=$\sqrt{\frac{2H}{7g}}$
(2)根据反射角等于入射角知,小球落在斜面上时的速度方向与水平方向成α角.
由图得 $\frac{{v}_{y}′}{{v}_{0}}$=tan60°
平抛运动过程,水平方向有:
x′=v0t′
竖直方向有:h1′=$\frac{{v}_{y}′}{2}t′$
由上得 x′=$\frac{2}{\sqrt{3}}$h1′
而 h2′=x′tan60°=$\frac{2}{3}$h1′
又 h2′+$\frac{2}{3}$h1′=H
解得 h1′=$\frac{3}{5}$H,x′=$\frac{2\sqrt{3}}{5}$H
由 h1′=$\frac{1}{2}gt{′}^{2}$,得 t′=$\sqrt{\frac{6H}{5g}}$
小球落在斜面上时竖直分速度 vy′=gt′=$\sqrt{\frac{6}{5}gH}$
水平分速度 v0=$\frac{x′}{t′}$=$\sqrt{\frac{2}{5}gH}$
小球第1次碰撞时速度的大小为 v1′=$\sqrt{{v}_{0}^{2}+{v}_{y}{′}^{2}}$=$\sqrt{\frac{8}{5}gH}$=2$\sqrt{\frac{2}{5}gH}$
(3)把此运动分解为平行于斜面与垂直于斜面两个方向.如图.
y轴上:小球先正向匀减速到0,然后返回与斜面相碰,以后重复,周期性往复运动,且运动周期为 T=$\frac{2v′sinα}{gcosα}$=4$\sqrt{\frac{6H}{5g}}$
x轴上做初速度为v′cosα、加速度为 gsinα的匀加速直线运动.
小球从第1次与斜面碰撞到第n次碰撞,历时 t0=(n-1)T
位移 x=v′cosα•t0+$\frac{1}{2}$gsinα$•{t}_{0}^{2}$
综上解得 x=$\frac{8\sqrt{3}}{5}$(n-1)(3n+1)H
答:
(1)小球在碰撞之前在空中飞行的时间为$\sqrt{\frac{2H}{7g}}$.
(2)如果小球与斜面碰撞后,恰好水平飞出,小球第1次碰撞时速度的大小是2$\sqrt{\frac{2}{5}gH}$;
(3)如果小球与斜面碰撞后,恰好水平飞出,小球从第1次与斜面碰撞到第n次碰撞时,小球的位移是$\frac{8\sqrt{3}}{5}$(n-1)(3n+1)H.
点评 利用平抛运动的规律,在水平和竖直方向列方程,同时要充分的利用三角形的边角关系,找出内在的联系.本题还要掌握平抛运动的两种分解方法,灵活选择解题方法.

 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案| A. | 4.5m/s | B. | 5m/s | C. | 6m/s | D. | 7.5m/s |
 如图所示,电源电动势为ε,电源内阻为r,当电键K闭合时,正确的判断是( )
如图所示,电源电动势为ε,电源内阻为r,当电键K闭合时,正确的判断是( )| A. | 电压表的读数变小,电流表的读数变小 | |
| B. | 电压表的读数变小,电流表的读数增大 | |
| C. | 电压表的读数增大,电流表的读数变小 | |
| D. | 电压表的读数增大,电流表的读数增大 |
| t (s)末 | 0 | 1 | 2 | 3 | 4 | 5 |
| x(m) | 0 | 5 | -4 | -1 | -7 | 1 |
| A. | 第1 s内 | B. | 第2 s内 | C. | 第3 s内 | D. | 第4 s内 |
| A. | 周期逐渐变大 | B. | 两星之间的万有引力逐渐增大 | ||
| C. | 两星的向心加速度都逐渐减小 | D. | 角速度逐渐增大 |
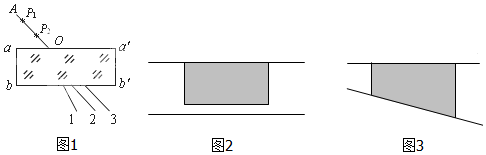
 如图所示为一由双刀双掷电键S、两节干电池(每节干电池的电动势E=1.5V,内阻r=1Ω)和一个小灯泡(额定电压为2.5V,额定电流为0.15A)组成的电路,那么:
如图所示为一由双刀双掷电键S、两节干电池(每节干电池的电动势E=1.5V,内阻r=1Ω)和一个小灯泡(额定电压为2.5V,额定电流为0.15A)组成的电路,那么: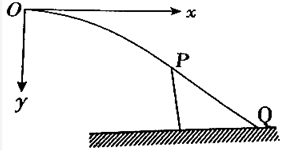 将小球以3m/s的速度水平抛出,它落地速度为5m/s,以vx、vy分别表示水平、竖直分速度,以ay表示竖直分加速度,取g=10m/s2,则图中正确的是( )
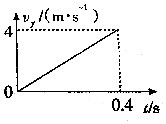
将小球以3m/s的速度水平抛出,它落地速度为5m/s,以vx、vy分别表示水平、竖直分速度,以ay表示竖直分加速度,取g=10m/s2,则图中正确的是( )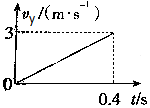
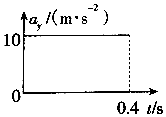
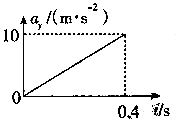
 在如图所示的竖直平面内,倾斜轨道与水平面的夹角θ=37°,空间有一匀强电场,电场方向垂直轨道向下,电场强度E=1.0×104N/C.小物体A质量m=0.2kg、电荷量q=+4×10-5C,若倾斜轨道足够长,A与轨道间的动摩擦因数为μ=0.5,A自斜面底端以4.4m/s的初速度沿斜面上滑,A在整个过程中电荷量保持不变,不计空气阻力(取g=10m/s2,sin37°=0.6,cos37°=0.8).求:
在如图所示的竖直平面内,倾斜轨道与水平面的夹角θ=37°,空间有一匀强电场,电场方向垂直轨道向下,电场强度E=1.0×104N/C.小物体A质量m=0.2kg、电荷量q=+4×10-5C,若倾斜轨道足够长,A与轨道间的动摩擦因数为μ=0.5,A自斜面底端以4.4m/s的初速度沿斜面上滑,A在整个过程中电荷量保持不变,不计空气阻力(取g=10m/s2,sin37°=0.6,cos37°=0.8).求: