题目内容
如图所示，在等腰三角形abc区域内有垂直纸面向外的匀强磁场，d是ac上任意一点，e是bc上任意一点．大量相同的带电粒子从a点以相同方向进入磁场，由于速度大小不同，粒子从ac和bc上不同点离开磁场．不计粒子重力，则从c点离开的粒子在三角形abc磁场区域内经过的弧长和运动时间，与从d点和e点离开的粒子相比较（ ）
A．经过的弧长一定大于从d点离开的粒子经过的弧长
B．经过的弧长一定小于从e点离开的粒子经过的弧长
C．运动时间一定大于从d点离开的粒子的运动时间
D．运动时间一定大于从e点离开的粒子的运动时间
【答案】分析：画出带点粒子在磁场中运动的轨迹，找出其圆心与半径，根据几何关系及周期公式即可判断．
解答：解：如图所示，
若粒子从ac边射出，粒子依次从ac上射出时，半径增大而圆心角相同，弧长等于半径乘以圆心角，所以经过的弧长越来越大，运动时间t=
，运动时间相同，所以A正确，C错误；
同理若粒子从bc边射出，粒子依次从bc上射出时，弧长越来越大，而圆心角越来越大，所以时间越来越长，故B错误，D正确．
故选AD
点评：解决带点粒子在磁场中运动的问题要画出其运动轨迹，找出相应的几何关系，从而确定圆心和半径．
解答：解：如图所示，
若粒子从ac边射出，粒子依次从ac上射出时，半径增大而圆心角相同，弧长等于半径乘以圆心角，所以经过的弧长越来越大，运动时间t=
，运动时间相同，所以A正确，C错误；同理若粒子从bc边射出，粒子依次从bc上射出时，弧长越来越大，而圆心角越来越大，所以时间越来越长，故B错误，D正确．
故选AD
点评：解决带点粒子在磁场中运动的问题要画出其运动轨迹，找出相应的几何关系，从而确定圆心和半径．
练习册系列答案
相关题目
（2013?开封模拟）如图所示，等腰直角三角体OCD由不同材料A、B拼接而成，P为两材料在CD边上的交点，且DP＞CP．现OD边水平放置，让小物块从C滑到D；然后将OC边水平放置，再让小物块从D滑到C，小物块两次滑动到达P点的时间相同．下列说法正确的是（ ）
如图所示，等腰直角三角体OCD由不同材料A、B拼接而成，P为两材料在CD边上的交点，且DP＞CP．现将OD边水平放置，让小物块无初速从C滑到D；然后将OC边水平放置，再让小物块无初速从D滑到C．已知小物块两次滑动到达P点的时间相同．下列说法正确的是（ ）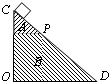
如图所示，等腰直角三角体OCD由不同材料A、B拼接而成，P为两材料在CD边上的交点，且DP＞CP．现OD边水平放置，让小物块无初速从C滑到D；然后将OC边水平放置，再让小物块无初速从D滑到C，小物块两次滑动到达P点的时间相同．下列说法正确的是（ ）
（2011?上海模拟）如图所示，等腰直角三角体OCD由不同材料A、B拼接而成，P为两材料在CD边上的交点，且DP＞CP．现OD边水平放置，让小物块从C滑到D；然后将OC边水平放置，再让小物块从D滑到C，小物块两次滑动经过P点的时间相同．下列说法正确的是（ ）