Question

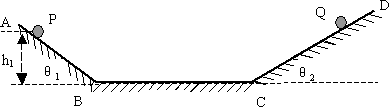
如图所示，倾角θ₁=37°的光滑斜面AB与倾角θ₂=30°的光滑斜面DC通过一段长度为2.2m的光滑水平面BC连接（连接处有一段很短的光滑圆弧相接）．现将一个质量为m₁=0.5kg的小球P从AB斜面上距地高度为h₁=1.8m处自由释放，同时将另一个质量为m₂的小球Q从DC斜面上某点处自由释放，若要使两小球同时进入水平面，且不断地在水平面上同一点发生相向碰撞（碰撞时无机械能损失）．试求：

（1）小球自由释放时，距地面高度h₂是多少？
（2）P、Q两球在BC面上碰撞的位置在何处？
（3）小球Q的质量m ₂ 是多少？

Answer 1

分析：（1）由题，两小球同时进入水平面，两球在斜面上运动的时间相等，根据牛顿第二定律分别求出两球的加速度，再根据位移公式列式求解．
（2）由速度公式求出两球在水平面滑动的速度大小，由位移公式结合两者在水平面上位移之和等于BC，即可求解．
（3）两球碰撞过程，无机械能损失，动量和机械能均守恒，根据两大守恒定律列式得到碰后两球的速度，为了使碰撞不断进入下去，碰撞后两球速度大小不变，方向反向，即可求解．

解答：解：（1）在斜面上小球P、Q的加速度分别为a₁和a₂，两球滚下的时间均为t，根据牛顿第二定律得：
    a₁=

mgsinθ1

m

=gsinθ₁=6m/s²，
    a₂=

mgsinθ2

m

=gsinθ₂=5m/s²，
由运动学公式得

h1

sinθ1

=

1

2

a1t2  可得t=

2h1 a1sinθ1

=

2×1.8 6×sin37°

=1s，
再由

h2

sinθ2

=

1

2

a2t2 
可得h₂=

1

2

a2sinθ2t2=

1

2

×5×sin30°×12m=1.25m
（2）到达斜面底端时，小球P、Q的速度分别为v₁=a₁t=6m/s，v₂=a₂t=5m/s，设碰撞点距B点x处，则应有
 x=v₁t，
2.2-x=v₂t，
联立可得x=1.2m．
（3）设两球P、Q碰后的速度为v₁₀和v₂₀，选取碰前P的速度v₁的方向为正方向，则有
  m₁v₁+m₂（-v₂）=m₁v₁₀+m₂v₂₀，
且有

1

2

m1

v

2 1

+

1

2

m2

v

2 2

=

1

2

m₁v

2 10

+

1

2

m2

v

2 20

，
为使碰撞不断地进行下去，碰后应有v₁₀=-v₁，v₂₀=-v₂，
故可解得：m₂=0.6kg．
答：
（1）小球自由释放时，距地面高度h₂是1.25m．
（2）P、Q两球在BC面上碰撞的位置在距B点1.2m处．
（3）小球Q的质量m₂是0.6kg．

点评：解决本题要紧扣题设条件：斜面上时间相等，运用力学基本的方法：牛顿第二定律和运动学公式进行求解h₂．关键是抓住弹性碰撞的规律：动量守恒和机械能守恒，进而求解小球Q的质量．