题目内容
已知某星球半径为R，表面重力加速度为a，不考虑星球自转的影响．万有引力常量为G，
（1）求该星球的质量M？
（2）若卫星绕星球做匀速圆周运动周期为T，求此卫星距星球表面高度h？
（1）求该星球的质量M？
（2）若卫星绕星球做匀速圆周运动周期为T，求此卫星距星球表面高度h？
分析：（1）由星球表面万有引力等于重力可得星球质量．
（2）由万有引力提供向心力的周期表达式，可得卫星的离地高度．
（2）由万有引力提供向心力的周期表达式，可得卫星的离地高度．
解答：解：（1）设星球的质量为M，在星球表面：
G
=ma
解得：
M=
（2）卫星在离地面高度为h处做匀速圆周运动，万有引力提供向心力：
G
=m(R+h)
解得：
h=
-R
答：（1）该星球的质量M=
．（2）此卫星距星球表面高度h=
-R．
G
| Mm |
| R2 |
解得：
M=
| aR2 |
| G |
（2）卫星在离地面高度为h处做匀速圆周运动，万有引力提供向心力：
G
| Mm |
| (R+h)2 |
| 4π2 |
| T2 |
解得：
h=
| 3 |
| ||
答：（1）该星球的质量M=
| aR2 |
| G |
| 3 |
| ||
点评：本题首先明确在星球表面万有引力等于重力，其次要会用万有引力提供向心力的各种表达式，基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
竖直向上抛出一个小球，小球能上升的最大高度为H，则（不考虑地球自转的影响）。
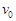竖直向上抛出一个小球，小球能上升的最大高度为H，则（不考虑地球自转的影响）。