题目内容
4．如图所示，O、A、B、C为同一直线上的四点，且2AB=BC．一质点自O点由静止出发，沿此直线做匀加速直线运动，依次经过A、B、C那三点，已知质点经过AB段所用时间为t1，通过BC段所用时间为t2，求质点由O点运动到A点所用的时间．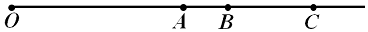
分析 根据平均速度推论分别求出AB段和BC段中间时刻的瞬时速度，结合速度时间公式求出加速度的表达式，从而得出A点速度的表达式，根据速度时间公式求出质点由O点运动到A点所用的时间．
解答 解：设AB=x，加速度为a，AB中间时刻的速度为v1，BC中间时刻的速度为v2，A点的速度为v，
由平均速度推论知：${v}_{1}=\overline{{v}_{1}}=\frac{x}{{t}_{1}}$，${v}_{2}=\overline{{v}_{2}}=\frac{2x}{{t}_{2}}$，
加速度为：a=$\frac{△v}{△t}$=$\frac{{v}_{2}-{v}_{1}}{\frac{{t}_{1}}{2}+\frac{{t}_{2}}{2}}$=$\frac{2x（2{t}_{1}-{t}_{2}）}{（{t}_{1}+{t}_{2}）{t}_{1}{t}_{2}}$，
则A点的速度为：v=${v}_{1}-a\frac{{t}_{1}}{2}$=$\frac{x（{{t}_{2}}^{2}+2{t}_{1}{t}_{2}-2{{t}_{1}}^{2}）}{{t}_{1}{t}_{2}（{t}_{1}+{t}_{2}）}$，
由O点运动到A点所用的时间为：t=$\frac{v}{a}$=$\frac{（{{t}_{2}}^{2}+2{t}_{1}{t}_{2}-2{{t}_{1}}^{2}）}{2（2{t}_{1}-{t}_{2}）}$．
答：质点由O点运动到A点所用的时间为$\frac{（{{t}_{2}}^{2}+2{t}_{1}{t}_{2}-2{{t}_{1}}^{2}）}{2（2{t}_{1}-{t}_{2}）}$．
点评 解决本题的关键掌握匀变速直线运动的运动学公式和推论，并能灵活运用，有时运用推论求解会使问题更加简捷．
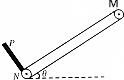如图所示，一倾斜传送带与水平面的倾角θ=37°，以v=10m/s的速率逆时针方向匀速运行，M、N为传送带的两个端点，MN两点间的距离L=5m，N端有一离传送带很近的弹性挡板P，在传送带上的M处由静止释放质量为1kg的木块（可视为质点），木块与传送带间的动摩擦因数μ=0.5，木块由静止释放后沿传送带向下运动，并与挡板P发生碰撞．已知碰撞时间极短，木块与挡板P碰撞后速度大小为碰撞前的一半，sin37°=0.6，g取10m/s2．传送带与轮子间无相对滑动，不计轮轴处的摩擦．求：| A． | 乙车在运动过程中的最大速度与a1、a2有关 | |
| B． | A、B两点的长度为v0t | |
| C． | 不论a1、a2为何值，都有$\frac{{{a_1}{a_2}}}{{{a_1}+{a_2}}}=\frac{{2{v_0}}}{t}$ | |
| D． | 不论a1、a2为何值，都有$\frac{{{a_1}{a_2}}}{{{a_1}+{a_2}}}=\frac{v_0}{t}$ |
| A． | 物体在2s末的速度为4m/s | |
| B． | 物体在2s内的位移为8m | |
| C． | 物体4s末的速度一定比3s末的速度大2m/s | |
| D． | 物体在2s内的平均速度为4m/s |
| A． | 1：1 | B． | 2：1 | C． | 3：2 | D． | 4：1 |
在相距L=1.2m的A、B两点各放一个点电荷Q1、Q2，Q1=+4.0×10-6C，在AB之间距B点0.4m的C点放入一个电量q=1.0×10-6C的点电荷，受力恰好平衡．则Q2应该带正电（填“正”或“负”），电量为1.0×10-6C．
如图所示，水平地面上放着一块木板，上面放一个木块，设木块对木板的压力为N，木块所受摩擦力为f．若使木块的B端逐渐升高时，A端不动，木块仍静止，则下列说法正确的是（ ）| A． | N增大，f增大 | B． | N增大，f减小 | C． | N减小，f增大 | D． | N减小，f减小 |