��Ŀ����
��16�֣��ڹ⻬��Ե��ˮƽ���Ͻ�����ͼ��ʾ��ƽ��ֱ������ϵ���ڴ�ˮƽ���Ͽ���Ϊ�ʵ�IJ�����С��a��ֹ������ϵ��ԭ����������Ϊ�ʵ�Ĵ�����С������ֹ������Ϊ��0����h����λ���ϣ��ּ�һ���������������糡ǿ�ȴ�СΪ������Χ�㹻�����ǿ�糡��ͬʱ��a����ijһ�ٶ�ʹ���������������˶�������������ϵԭ����ʱ�ٶ�Ϊv0����ʱ������ȥ�糡���ļ�һ����ֱ�ھ�Եˮƽ�����ϡ��Ÿ�Ӧǿ�ȴ�СΪ������Χ�㹻�����ǿ�ų���������������a����������
��1��b��ıȺ�![]() ��
��
��2��������ԭ������ʼ��������a�����������ʱ�� ��
 ��3������ӿ�ʼλ���˶���ԭ����ʱ��a���λ�� ��
��3������ӿ�ʼλ���˶���ԭ����ʱ��a���λ�� ��
��16�֣��⣺(1) �����ܵ糡���������ȼ����˶�,�ɶ��ܶ�����:
![]() (2��)
(2��)
 ������ıȺ�Ϊ
������ıȺ�Ϊ![]() ��1�֣�
��1�֣�
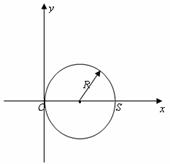
(2) �����˶���ԭ�����ˮƽ����������Բ���˶�
������![]() (1��)
(1��)
����![]() ��1�֣�
��1�֣�
�����ã�![]() ��1�֣�
��1�֣�
b��ֻ����a��������ͼ�е�S������������ʱ��Ϊ
![]() ��1�֣�
��1�֣�
![]() ���� (1��)
���� (1��)
(3) a��ʼ�˶�����b����������ʱ��Ϊ��![]() (1��)
(1��)
����![]() ��1�֣�
��1�֣�
a��ͨ����·��ΪOS=2R (1��)
���Կɵ�a����ٶȣ�v=![]() (1��)
(1��)
��v=![]() (1��)
(1��)
��a����x���ϵ�����Ϊ![]() (1��)
(1��)
![]() ���� ��1�֣�
���� ��1�֣�
a���λ��Ϊ��![]() �� 0�� ��1�֣�
�� 0�� ��1�֣�

 �ڹ⻬��Ե��ˮƽ���ϣ��ó�Ϊ2L�ľ�Ե�����������������Ϊm�Ĵ���С��A��B��A��Ĵ�����Ϊ+2q��B��Ĵ�����Ϊ-3q�����һ����ϵͳ����ͼ��ʾ������MPΪAB�������ߵĴ�ֱƽ���ߣ�����NQ��MPƽ�������4L�����A��B�ֱ�ֹ������MP�����࣬��MP�ľ����ΪL����A�������NQ�ľ���Ϊ3L������С��Ϊ�ʵ㣬������˵�������������MP��NQ�����ˮƽ���ҵ���ǿ�糡E�������ϵͳ�ӿ�ʼ�˶����ٶȵ�һ��Ϊ��B������ܵı仯����������
�ڹ⻬��Ե��ˮƽ���ϣ��ó�Ϊ2L�ľ�Ե�����������������Ϊm�Ĵ���С��A��B��A��Ĵ�����Ϊ+2q��B��Ĵ�����Ϊ-3q�����һ����ϵͳ����ͼ��ʾ������MPΪAB�������ߵĴ�ֱƽ���ߣ�����NQ��MPƽ�������4L�����A��B�ֱ�ֹ������MP�����࣬��MP�ľ����ΪL����A�������NQ�ľ���Ϊ3L������С��Ϊ�ʵ㣬������˵�������������MP��NQ�����ˮƽ���ҵ���ǿ�糡E�������ϵͳ�ӿ�ʼ�˶����ٶȵ�һ��Ϊ��B������ܵı仯���������� ��ͼ��ʾ���ڹ⻬��Ե��ˮƽ������һ����һ�����ȵ���Χ�ɵ��������߿�abcd����߳�ΪL���ܵ���ΪR�����ڴŸ�Ӧǿ��ΪB��������ֱ���µ���ǿ�ų�����ߣ�ͼ������MNΪ�ų�����߽磮�߿��ں��������������˶�������ab�߱�����MNƽ�У����߿����ٶ�v0����ų�����ʱ����ǡ���������˶�����
��ͼ��ʾ���ڹ⻬��Ե��ˮƽ������һ����һ�����ȵ���Χ�ɵ��������߿�abcd����߳�ΪL���ܵ���ΪR�����ڴŸ�Ӧǿ��ΪB��������ֱ���µ���ǿ�ų�����ߣ�ͼ������MNΪ�ų�����߽磮�߿��ں��������������˶�������ab�߱�����MNƽ�У����߿����ٶ�v0����ų�����ʱ����ǡ���������˶����� ��ͼ��ʾ���ڹ⻬��Ե��ˮƽ���Ϲ̶���������������A��B��O��ΪAB���ߵ��е㣬C��DΪAB�����Ϲ���0��ԳƵ������㣬��CO=OD=L��һ������Ŀ���Ϊ���ɵ�С���Գ��ٶ�v����C���˶���D�㣮��O��ĵ���?0=0��ȡC��Ϊ����ԭ�㣬����Ϊx����������������й���С��ĵ�����EP��С��Ķ���EK������?���糡ǿ��E��С���˶���λ��x�仯��ͼ������ȷ���ǣ�������
��ͼ��ʾ���ڹ⻬��Ե��ˮƽ���Ϲ̶���������������A��B��O��ΪAB���ߵ��е㣬C��DΪAB�����Ϲ���0��ԳƵ������㣬��CO=OD=L��һ������Ŀ���Ϊ���ɵ�С���Գ��ٶ�v����C���˶���D�㣮��O��ĵ���?0=0��ȡC��Ϊ����ԭ�㣬����Ϊx����������������й���С��ĵ�����EP��С��Ķ���EK������?���糡ǿ��E��С���˶���λ��x�仯��ͼ������ȷ���ǣ������� ��ͼ��ʾ���ڹ⻬��Ե��ˮƽ���ϣ���һ��ֹ��A������Ϊm=1��10-3kg���������С���ּ�һˮƽ�������ǿ�糡ʹС����A���˶���B�㣬����������ΪW=0.2J����֪A��B��������ΪL=0.1m�����Ʋ�ΪUAB=20V��
��ͼ��ʾ���ڹ⻬��Ե��ˮƽ���ϣ���һ��ֹ��A������Ϊm=1��10-3kg���������С���ּ�һˮƽ�������ǿ�糡ʹС����A���˶���B�㣬����������ΪW=0.2J����֪A��B��������ΪL=0.1m�����Ʋ�ΪUAB=20V�� �ڹ⻬��Ե��ˮƽ�����а�Բ���εİ���ABC������뾶ΪR=0.4m���ռ�����ֱ���µ���ǿ�糡��һ������m=0.02kg��������q=+l��0��l0-3 C��С����Ϊ�ʵ㣩�Գ��ٶ�v0=4m/s��A��ˮƽ���˰��ۣ�ǡ��ײ��D�㣬D��O��������ˮƽ����н�Ϊ��=53�㣬�������ٶ�ȡg=10m/s2��sin 53��=0.8��cos 53��=0.6������
�ڹ⻬��Ե��ˮƽ�����а�Բ���εİ���ABC������뾶ΪR=0.4m���ռ�����ֱ���µ���ǿ�糡��һ������m=0.02kg��������q=+l��0��l0-3 C��С����Ϊ�ʵ㣩�Գ��ٶ�v0=4m/s��A��ˮƽ���˰��ۣ�ǡ��ײ��D�㣬D��O��������ˮƽ����н�Ϊ��=53�㣬�������ٶ�ȡg=10m/s2��sin 53��=0.8��cos 53��=0.6������