��Ŀ����
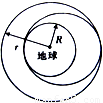
 �����յ�������Ҳ�����������ߺŷɴ��ı���˶�����ͼ��ʾ���ɴ�������������Ԥ������Բ�ι�����У�ijһʱ�̷ɴ��ڽ��ص��������������٣������϶�ʱ���ɴ��ٶ�����ת�Ƶ������������е���Բ������ɴ���Զ�ص���һ�ε����٣����ذ뾶Ϊ r ��Բ�ι���Ƶ����˶��������İ뾶ΪR�����������������ٶ�Ϊg�������ƿ��������������������ߺŴӽ��ص��˶���Զ�ص��ʱ�䣨���ʱ�䣩��
�����յ�������Ҳ�����������ߺŷɴ��ı���˶�����ͼ��ʾ���ɴ�������������Ԥ������Բ�ι�����У�ijһʱ�̷ɴ��ڽ��ص��������������٣������϶�ʱ���ɴ��ٶ�����ת�Ƶ������������е���Բ������ɴ���Զ�ص���һ�ε����٣����ذ뾶Ϊ r ��Բ�ι���Ƶ����˶��������İ뾶ΪR�����������������ٶ�Ϊg�������ƿ��������������������ߺŴӽ��ص��˶���Զ�ص��ʱ�䣨���ʱ�䣩���������������������ṩ�������������������������Ϳ����յ������������з��̼�����⣮
����⣺���ɴ��ذ뾶Ϊr��Բ�ι���Ƶ����˶�ʱ���������������ṩ����������
=mr(
)2
����T2=
����
���ݿ����յ������ɣ�
=��������
=
����
��������
=mg ��GM=gR2����
�ɢ٢ڢ۽�ã�
t=
�������ߺŴӽ��ص��˶���Զ�ص��ʱ��Ϊt=
��
| GMm |
| r2 |
| 2�� |
| T |
����T2=
| 2��r3 |
| GM |
���ݿ����յ������ɣ�
| a3 |
| T2 |
| r3 |
| T2 |
(
| ||
| (2t)2 |
��������
| GMm |
| R2 |
�ɢ٢ڢ۽�ã�
t=
| ��(R+r) |
| 2R |
|
�������ߺŴӽ��ص��˶���Զ�ص��ʱ��Ϊt=
| ��(R+r) |
| 2R |
|
���������ⲻ�������������ṩ�������������������������Ĺ�ϵʽ������Ҫ������յ������ɣ����������������⣮

��ϰ��ϵ�д�
 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
�����Ŀ