Question

一玻璃立方体中心有一点状光源．今在立方体的部分表面镀上不透明薄膜，以致从光源发出的光线只经过一次折射不能透出立方体．已知该玻璃的折射率为

2

，求镀膜的面积与立方体表面积之比的最小值．

Answer 1

分析：通过光线在镀膜部分发生全反射，根据临界情况，通过几何关系求出镀膜面积与立方体表面积之比的最小值．

解答：解：如图，考虑从玻璃立方体中心O点发出的一条光线，假设它斜射到玻璃立方体上表面发生折射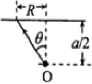
根据折射定律有nsinθ=sinα    
式中，n是玻璃的折射率，入射角等于θ，α是折射角
现假设A点是上表面面积最小的不透明薄膜边缘上的一点．由题意，在A点刚好发生全反射，故αA=

π

2

．
设线段OA在立方体上表面的投影长为R_A，由几何关系有sinθA=

RA

RA2+( a 2 )2

．
式中a为玻璃立方体的边长，有①②③式得RA=

a

2 n2-1

．
则RA=

a

2

    
由题意，上表面所镀的面积最小的不透明薄膜应是半径为R_A的圆．所求的镀膜面积S'与玻璃立方体的表面积S之比为

s′

s

=

6πRA2

6a2

=

π

4

．
答：镀膜的面积与立方体表面积之比的最小值为

π

4

．

点评：解决本题的关键确定临界情况，根据折射定律，通过几何关系进行求解．