题目内容
如图所示,坐标系xOy在竖直平面内,空间有沿水平方向垂直于纸面向外的匀强磁场,磁感应强度大小为B,在x>0的空间里有沿x轴正方向的匀强电场,场强的大小为E,一个带正电的小球经过图中的x轴上的A点,沿着与水平方向成θ=30°角的斜向下直线做匀速运动,经过y轴上的B点进入x<0的区域,要使小球进入x<0区域后能在竖直面内做匀速圆周运动,需在x<0区域另加一匀强电场,若带电小球做圆周运动通过x轴上的C点(C点未标出),且
=
,设重力加速度为g,求:
(1)小球运动速率的大小;
(2)在x<0的区域所加电场的场强大小和方向;
(3)小球从B点运动到C点所用时间.
| . |
| OA |
| . |
| OC |
(1)小球运动速率的大小;
(2)在x<0的区域所加电场的场强大小和方向;
(3)小球从B点运动到C点所用时间.

(1)小球从A运动到B的过程中,小球受重力、电场力和洛伦兹力作用而处于平衡状态,如图右图所示.由题设条件知sin30°=
,

所以小球的运动速率为 v=
.
(2)小球在x<0的区域做匀速圆周运动,则小球的重力与所受的电场力平衡,洛伦兹力提供做圆周运动的向心力.则
mg=qE,
又 tan30°=
.
所以 E′=
E,方向竖直向上.
(3)如图所示,连接BC,过B作AB的垂线交x轴于O′.

因为 θ=30°,所以∠AO′B=60°,又
=
,
故∠OCB=θ=30°,所以∠CBO′=30°,
=
,则O’为小球做圆周运动的圆心
且 qvB=m
,R=
,T=
=
,
由于∠CO′B=120°,
小球从点B运动到点C的时间为 t1=
T=
,
又
=
,所以
=
.t1=
答:
(1)小球运动速率的大小为
.
(2)在x<0的区域所加电场的场强大小为
E,方向竖直向上.
(3)小球从B点运动到C点所用时间是
.
| qE |
| Bqv |

所以小球的运动速率为 v=
| 2E |
| B |
(2)小球在x<0的区域做匀速圆周运动,则小球的重力与所受的电场力平衡,洛伦兹力提供做圆周运动的向心力.则
mg=qE,
又 tan30°=
| qE |
| mg |
所以 E′=
| 3 |
(3)如图所示,连接BC,过B作AB的垂线交x轴于O′.

因为 θ=30°,所以∠AO′B=60°,又
| . |
| OA |
| . |
| OC |
故∠OCB=θ=30°,所以∠CBO′=30°,
| . |
| O′C |
| . |
| O′B |
且 qvB=m
| v2 |
| R |
| mv |
| Bq |
| 2πR |
| v |
| 2πm |
| Bq |
由于∠CO′B=120°,
小球从点B运动到点C的时间为 t1=
| 1 |
| 3 |
| 2πm |
| 3Bq |
又
| m |
| q |
| ||
| g |
| . |
| OA |
2
| ||
| gB2 |
2
| ||
| 3gB |
答:
(1)小球运动速率的大小为
| 2E |
| B |
(2)在x<0的区域所加电场的场强大小为
| 3 |
(3)小球从B点运动到C点所用时间是
2
| ||
| 3gB |

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 (2005?福建模拟)如图所示,坐标系xOy在竖直平面内,空间有沿水平方向、垂直纸面向外的匀强磁场,磁感应强度为B.在x>0的空间内有沿x轴正方向的匀强电场,场强为E.一个带正电荷的小球经过图中x轴上的M点,沿着与水平方向成θ=30°角的斜向下的直线做匀速运动,经过y轴上的N点进入x<0的区域内.要使小球进入x<0区域后能在竖直面内做匀速圆周运动,需在x<0区域内另加一匀强电场.若带电小球做圆周运动通过y轴上的P点(P点未标出),重力加速度设为g,求:
(2005?福建模拟)如图所示,坐标系xOy在竖直平面内,空间有沿水平方向、垂直纸面向外的匀强磁场,磁感应强度为B.在x>0的空间内有沿x轴正方向的匀强电场,场强为E.一个带正电荷的小球经过图中x轴上的M点,沿着与水平方向成θ=30°角的斜向下的直线做匀速运动,经过y轴上的N点进入x<0的区域内.要使小球进入x<0区域后能在竖直面内做匀速圆周运动,需在x<0区域内另加一匀强电场.若带电小球做圆周运动通过y轴上的P点(P点未标出),重力加速度设为g,求: (2010?南开区一模)如图所示,坐标系xOy在竖直平面内,空间有沿水平方向垂直于纸面向外的匀强磁场,磁感应强度大小为B,在x>0的空间里有沿x轴正方向的匀强电场,场强的大小为E,一个带正电的小球经过图中的x轴上的A点,沿着与水平方向成θ=30°角的斜向下直线做匀速运动,经过y轴上的B点进入x<0的区域,要使小球进入x<0区域后能在竖直面内做匀速圆周运动,需在x<0区域另加一匀强电场,若带电小球做圆周运动通过x轴上的C点(C点未标出),且
(2010?南开区一模)如图所示,坐标系xOy在竖直平面内,空间有沿水平方向垂直于纸面向外的匀强磁场,磁感应强度大小为B,在x>0的空间里有沿x轴正方向的匀强电场,场强的大小为E,一个带正电的小球经过图中的x轴上的A点,沿着与水平方向成θ=30°角的斜向下直线做匀速运动,经过y轴上的B点进入x<0的区域,要使小球进入x<0区域后能在竖直面内做匀速圆周运动,需在x<0区域另加一匀强电场,若带电小球做圆周运动通过x轴上的C点(C点未标出),且 如图所示,坐标系xOy在竖直平面内,水平轨道AB和斜面BC均光滑且绝缘,AB和BC的长度均为L,斜面BC与水平地面间的夹角θ=60°,有一质量为m、电量为+q的带电小球(可看成质点)被放在A点.已知在第一象限分布着互相垂直的匀强电场和匀强磁场,电场方向竖直向上,场强大小
如图所示,坐标系xOy在竖直平面内,水平轨道AB和斜面BC均光滑且绝缘,AB和BC的长度均为L,斜面BC与水平地面间的夹角θ=60°,有一质量为m、电量为+q的带电小球(可看成质点)被放在A点.已知在第一象限分布着互相垂直的匀强电场和匀强磁场,电场方向竖直向上,场强大小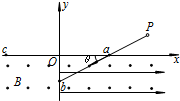 如图所示,坐标系xOy在竖直平面内,x轴正方向水平向右,y轴正方向竖直向上.y<0的区域有垂直于坐标平面向外的匀强磁场,磁感应强度大小为B;在第一象限的空间内有与x轴平行的匀强电场(图中未画出);第四象限有与x轴同方向的匀强电场;第三象限也存在着匀强电场(图中未画出).一个质量为m、电荷量为q的带电微粒从第一象限的P点由静止释放,恰好能在坐标平面内沿与x轴成θ=30°角的直线斜向下运动,经过x轴上的a点进入y<0的区域后开始做匀速直线运动,经过y轴上的b点进入x<0的区域后做匀速圆周运动,最后通过x轴上的c点,且Oa=Oc.已知重力加速度为g,空气阻力可忽略不计,求:
如图所示,坐标系xOy在竖直平面内,x轴正方向水平向右,y轴正方向竖直向上.y<0的区域有垂直于坐标平面向外的匀强磁场,磁感应强度大小为B;在第一象限的空间内有与x轴平行的匀强电场(图中未画出);第四象限有与x轴同方向的匀强电场;第三象限也存在着匀强电场(图中未画出).一个质量为m、电荷量为q的带电微粒从第一象限的P点由静止释放,恰好能在坐标平面内沿与x轴成θ=30°角的直线斜向下运动,经过x轴上的a点进入y<0的区域后开始做匀速直线运动,经过y轴上的b点进入x<0的区域后做匀速圆周运动,最后通过x轴上的c点,且Oa=Oc.已知重力加速度为g,空气阻力可忽略不计,求: 如图所示,坐标系xOy在竖直平面内,光滑且绝缘的水平轨道MN的长度为L,N点到O点的竖直距
如图所示,坐标系xOy在竖直平面内,光滑且绝缘的水平轨道MN的长度为L,N点到O点的竖直距