一电子(e.m)以速度v0与x轴成30°角垂直射入磁感强度为B的匀强磁场中.经一段时间后.打在x轴上的P点.如图所示.则P点到O点的距离为多少?电子由O点运动到P点所用的时间为多少? 题目和参考答案——青夏教育精英家教网—

题目内容

一电子（e，m）以速度v₀与x轴成30°角垂直射入磁感强度为B的匀强磁场中，经一段时间后，打在x轴上的P点，如图所示，则P点到O点的距离为多少？电子由O点运动到P点所用的时间为多少？

分析：（1）先根据几何关系求出P点到O点的距离等于半径，再根据洛伦兹力提供向心力求出半径；
（2）由几何关系得出运动的圆心角，再根据与周期的关系求出运动时间．

解答：解：（1）电子在磁场中受洛伦兹力作用做匀速圆周运动，轨迹如图所示：

由图可知：弦切角为30°，所以圆心角为60°
P点到O点的距离等于半径，
根据Bev₀=

mv2

得：R=

所以P点到O点的距离等于

（2）圆周运动的周期T=

2πR

2πm

圆心角为60°，所以电子由O点运动到P点所用的时间：t=

60°

360°

πm

3eB

答：则P点到O点的距离为

，电子由O点运动到P点所用的时间为

πm

3eB

．

点评：本题是粒子在磁场中圆周运动的轨迹问题，关键是运用几何知识画出轨迹、求出半径．

练习册系列答案

相关题目

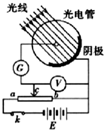（1）用如图所示的装置研究光电效应现象，用光子能量为2.5eV的光照射到光电管上时，电流表G示数不为0，移动变阻器的触点c，当电压表的示数大于或等于时0.7V，电流表示数为0，则

A．光电管阴极的逸出功为1.8eV
B．电键k断开后，有电流流过电流表G
C．光电子的最大初动能为0.7eV
D．改用能量为1.5eV的光子照射，电流表G也有电流，但电流较小
（2）下列说法正确的是

A．甲、乙两个物体组成一系统，甲、乙所受合外力不均为零，则系统的动量不可能守恒
B．用不可见光照射金属一定比用可见光照射同种金属产生的光电子的初动能要大
C．波粒二象性中的波动性是大量光子和高速运动的微观粒子的行为，这种波动性与机械波在本质上是不同的
D．欲使处于基态的氢原子电离，可以用动能为13.7eV的电子去碰撞
E．原子核式结构模型是由汤姆逊在α粒子散射实验基础上提出的
F．发现中子的核反应是

Be+

He→

C+

n
G．核力是强相互作用的一种表现，任意两个核子之间都存在核力作用
H．β衰变说明了β粒子（电子）是原子核的组成部分
（3）质量分别为2m和m的A、B两个小球在光滑的水平面上分别以速度v₁、v₂同向运动并发生对心碰撞，碰后B球被右侧的墙原速弹回，又与A相碰，碰后两球都静止，则第一次碰后A球的动量大小P_A

（填“＞”“=”或“＜”）B球动量大小P_B，第一次碰后B球速度为

．

速调管是用于甚高频信号放大的一种装置（如图1所示），其核心部件是由两个相距为s的腔组成，其中输入腔由一对相距为l的平行正对金属板构成（图中虚线框内的部分）。已知电子的质量为m，电荷量为e，为计算方便，在以下的讨论中电子之间的相互作用力及其重力均忽略不计。

（1）若输入腔中的电场保持不变，电子以一定的初速度v₀从A板上的小孔沿垂直A板的方向进入输入腔，而由B板射出输入腔时速度减为v₀/2，求输入腔中的电场强度E的大小及电子通过输入腔电场区域所用的时间t；

（2）现B板接地（图中未画出），在输入腔的两极板间加上如图2所示周期为T的高频方波交变电压，在t=0时A板电势为U₀，此此同时电子以速度v₀连续从A板上的小孔沿垂直A板的方向射入输入腔中，并能从B板上的小孔射出，射向输出腔的C孔。若在nT~(n + 1)T的时间内(n = 0，1，2，3，……)，前半周期经B板射出的电子速度为v₁（未知），后半周期经B板射出的电子速度为v₂（未知），求v₁和v₂的比值；（由于输入腔内极板间距离很小，且电子的速度很大，因此电子通过输入腔的时间忽略不计）

（3）在上述速度分别为v₁和v₂的电子中，若t时刻经过B板射出的速度为v₁的电子总能与时刻经B板射出的速度为v₂的电子同时进入输出腔，则可通过相移器的控制将电子的动能转化为输出腔中的电场能，从而实现对甚高频信号进行放大的作用。为实现上述过程，输出腔的C孔到输入腔的右极板B的距离s应满足什么条件？

图1 图2

速调管是用于甚高频信号放大的一种装置(如图甲所示)，其核心部件是由两个相距为s的腔组成，其中输入腔由一对相距为l的平行正对金属板构成(图中虚线框内的部分).已知电子的质量为m，电荷量为e，为计算方便，在以下的讨论中电子之间的相互作用力及其重力均忽略不计.

(1)若输入腔中的电场保持不变，电子以一定的初速度v₀从A板上的小孔沿垂直A板的方向进入输入腔，而由B板射出输入腔时速度减为v₀／2，求输入腔中的电场强度E的大小及电子通过输入腔电场区域所用的时间t；

(2)现B板接地(图中未画出)，在输入腔的两极板间加上如图乙所示周期为了的高频方波交变电压，在t=0时A板电势为U₀，与此同时电子以速度询连续从A板上的小孔沿垂直A板的方向射入输入腔中，并能从B板上的小孔射出，射向输出腔的C孔.若在nT—(n+1)T的时间内(n=0，1，2，3，…)，前半周期经B板射出的电子速度为v₁(未知)，后半周期经B板射出的电子速度为v₂(未知)，求v₁和v₂的比值；(由于输入腔内极板间距离很小，且电子的速度很大，因此电子通过输入腔的时间忽略不计)

(3)在上述速度分别为v₁和v₂的电子中，若t时刻经过B板射出的速度为v₁的电子总能与t+时刻经B板射出的速度为v₂的电子同时进入输出腔，则可通过相移器的控制将电子的动能转化为输出腔中的电场能，从而实现对甚高频信号进行放大的作用，为实现上述过程，输出腔的C孔到输入腔的右极板B的距离s应满足什么条件？

【选做题】本题包括A、B、C三小题，请选定其中两题，并在答题卡相应的答题区域内作答．若三题都做，则按A、B两题评分．

A．(选修模块3—3)（12分）

（1）在研究性学习的过程中，针对能源问题，大气污染问题同学们提出了如下四个活动方案，哪些从理论上讲是可行的

（A）发明一种制冷设备，使温度降至绝对零度以下

（B）汽车尾气中各类有害气体排入大气后严重污染了空气，想办法使它们自发地分离，既清洁了空气，又变废为宝

（C）某国际科研小组正在研制利用超导材料制成灯泡的灯丝和闭合电路．利用电磁感应激起电流后，由于电路电阻为零从而使灯泡一直发光

（D）由于太阳的照射，海洋表面的温度可达30℃左右，而海洋深处的温度要低得多，在水600～1000m的地方，水温约为4℃．据此，科学家研制了一种抗腐蚀的热交换器，利用海水温差发电

（2）秋天附着在树叶上的露水常呈球形，.这是因为____▲____．水银放在某一固体容器中，其液面向下弯，说明水银__▲___这种固体（填“浸润”或“ 不浸润”）．

（3）如图所示，在竖直放置绝热圆柱形容器内用质量为m的绝热活塞密封一部分气体，活塞与容器壁间能无摩擦滑动，容器的横截面积为S，开始时密闭气体的温度为T₀，活塞与容器底的距离为h₀．现将整个装置放在大气压恒为P₀的空气中，当气体从外界吸收热量Q后，活塞缓慢上升d后再次平衡，问：

①此时密闭气体的温度是多少？

②在此过程中密闭气体的内能增加了多少？

B．(选修模块3—4)（12分）

（1）下列说法中正确的有 ▲ ．

（A）2010年4月14日早晨7时49分，青海省玉树藏族自治州玉树县发生7.1级地震，造成重大人员财产损失，地震波是机械波，地震波中既有横波也有纵波

（B）太阳能真空玻璃管采用镀膜技术增加透射光，这是利用了光的衍射原理

（C）相对论认为：真空中的光速在不同惯性参照系中是不相同的

（D）医院里用于检测的“彩超”的原理是：向病人体内发射超声波，经血

液反射后被接收，测出反射波的频率变化，就可知血液的流速．这

一技术应用了多普勒效应

（2）如图所示为一列简谐波在t₁=0时刻的图象，此时波中质点M的运动方

向沿y轴负方向，且到t₂=0.55s质点M恰好第3次到达y轴正方向最大

位移处，该波的传播方向为__▲___，波速为___▲____m／s．

（3）如图所示是一种折射率n=1.5的棱镜．现有一束光线沿MN的方向射

到棱镜的AB界面上，入射角的大小．求光在棱镜中传

播的速率及此束光线射出棱镜后的方向（不考虑返回到AB面上的光线）．

C．(选修模块3—5)（12分）

（1）下列说法中正确的有___▲____．

（A）黑体辐射时电磁波的强度按波长的分布只与黑体的温度有关

（B）普朗克为了解释光电效应的规律，提出了光子说

（C）天然放射现象的发现揭示原子核有复杂的结构

（D）卢瑟福首先发现了质子和中子

（2）如图所示是使用光电管的原理图．当频率为v的可见光照射到阴极K上时，

电流表中有电流通过．

①当变阻器的滑动端P向 ▲ 滑动时（填“左”或“右”），通过电流表的电流将会减小．

②当电流表电流刚减小到零时，电压表的读数为U，则光电子的最大初动能为

▲ （已知电子电荷量为e）．

③如果不改变入射光的频率，而增加入射光的强度，则光电子的最大初动能将__▲___

（填“增加”、“减小”或“不变”）．

（3）一炮弹质量为m，以一定的倾角斜向上发射，到达最高点时速度为v，炮弹在最高点爆炸成两块，

其中一块恰好做自由落体运动，质量为．则另一块爆炸后瞬时的速度大小__▲__。