题目内容
如图所示，两个半径不同而内壁光滑的半圆轨道固定于地面，一个小球先后从与球心在同一水平高度的A、B两点由静止开始自由下滑，通过轨道最低点时（ ）分析：小球从与球心在同一水平高度的A、B两点由静止开始自由下滑过程中，受到重力和支持力作用，但只有重力做功，机械能守恒，由机械能守恒定律可求出小球到最低点的速度，然后由向心加速度公式求向心加速度，由牛顿第二定律求出支持力，进而来比较向心加速度大小和压力大小．
解答：解：A、设半圆轨道的半径为r，小球到最低点的速度为v，由机械能守恒定律得：
mgr=
mv2…①
在最低点，由牛顿第二定律得：
F-mg=m
…②
联立①②解得：FN=3mg
由牛顿第三定律知压力为3mg，与半径无关，所以小球对轨道的压力相同．因此，A正确，B错误．
C、小球的向心加速度为：an=
…③
联立①③两式解得：an=2g，加速度与半径无关，因此此时小球的向心加速度相等，所以C错误．
D、由上可知，D错误．
故选：A
mgr=
| 1 |
| 2 |
在最低点，由牛顿第二定律得：
F-mg=m
| v2 |
| r |
联立①②解得：FN=3mg
由牛顿第三定律知压力为3mg，与半径无关，所以小球对轨道的压力相同．因此，A正确，B错误．
C、小球的向心加速度为：an=
| v2 |
| r |
联立①③两式解得：an=2g，加速度与半径无关，因此此时小球的向心加速度相等，所以C错误．
D、由上可知，D错误．
故选：A
点评：小球下滑，机械能守恒，机械能守恒定律、牛顿第二定律、向心力公式分别求出小球在最低点的压力和向心加速度，可以看出它们与圆轨道的半径无关．
练习册系列答案
考前必练系列答案
相关题目
如图所示，两个半径不同而内壁光滑的半圆轨道固定于地面，两个质量不同的小球分别从与球心在同一水平高度的A、B两点由静止开始下滑，空气阻力不计，通过轨道最低点时（ ）
如图所示，两个半径相等的半圆形光滑轨道置于竖直平面内，左右两端点等高，它们分别处于竖直向下和水平向左的匀强电场中，匀强电场的电场强度大小相同．两个相同的带正电小球同时从两轨道左端最高点由静止释放，两球均可到达轨道的最低点，M、N分别为两轨道的最低点，则下列说法中正确的是（ ）
如图所示，两个半径相同的半圆型光滑轨道分别竖直放在匀强电场和匀强磁场中，轨道两端在同一高度上，两个相同的带正电小球同时从两轨道左端最高点由静止释放，M、N为轨道的最低点（ ）
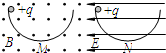如图所示，两个半径相同的半圆形轨道分别竖直放在匀强电场和匀强磁场中，轨道两端在同一高度上，轨道是光滑的．两个相同的带正电小球同球从两轨道左端最高点由静止释放，M、N为轨道的最低点，则（ ）| A、两小球到达轨道最低点的速度vM=vN | B、两小球到达轨道最低点时对轨道的压力FM＞FN | C、小球第一次到达M点的时间大于小球第一次到达N点的时间 | D、在磁场中小球能到达轨道的另一端，在电场中小球不能到达轨道的另一端 |