题目内容
15. 如图所示,两根足够长、电阻不计且相距L=0.2m的平行金属导轨固定在倾角θ=37°的绝缘斜面上,顶端接有一个额定电压U=4V的小灯泡,两导轨间有一磁感应强度大小B=5T、方向垂直斜面向上的匀强磁场.今将一根长为2L、质量m=0.2kg、电阻
如图所示,两根足够长、电阻不计且相距L=0.2m的平行金属导轨固定在倾角θ=37°的绝缘斜面上,顶端接有一个额定电压U=4V的小灯泡,两导轨间有一磁感应强度大小B=5T、方向垂直斜面向上的匀强磁场.今将一根长为2L、质量m=0.2kg、电阻r=1.0Ω的金属棒垂直于导轨放置在顶端附近无初速度释放,金属棒与导轨接触良好,金属棒与导轨间的动摩擦因数μ=0.25,已知金属棒下滑到速度稳定时,小灯泡恰能正常发光,重力加速度g取10m/s2,sin 37°=0.6,cos 37°=0.8.求:
(1)金属棒刚开始运动时的加速度大小.
(2)金属棒稳定下滑时的速度大小.
分析 (1)金属棒刚开始运动时,初速度为零,安培力为零,结合牛顿第二定律求出金属棒刚开始运动时的加速度大小.
(2)金属棒稳定时做匀速直线运动,结合平衡,以及安培力公式、感应电动势公式和闭合电路欧姆定律求出金属棒稳定时的速度.
解答 解:(1)金属棒刚开始运动时初速度为零,不受安培力作用,由牛顿第二定律得:
mgsin θ-μmgcos θ=ma,
代入数据得:a=4 m/s2.
(2)设金属棒稳定下滑时的速度为v,感应电动势为E(金属棒的有效长度为L),回路中的电流为I,由平衡条件得:mgsin θ=BIL+μmgcos θ ①
由闭合电路欧姆定律得I=$\frac{E-U}{r}$ ②
由法拉第电磁感应定律得E=BLv ③
联立①②③解得:v=4.8 m/s.
答:(1)金属棒刚开始运动时的加速度大小为4m/s2.
(2)金属棒稳定下滑时的速度大小为4.8m/s.
点评 本题是电磁感应与力学知识的综合应用,关键是安培力的分析和计算,它是联系力学与电磁感应的桥梁.

练习册系列答案
相关题目
17.如图甲所示,甲、乙两个小球可视为质点,甲球沿倾角为30°的光滑足够长斜面由静止开始下滑,乙球做自由落体运动,甲、乙两球的动能与路程的关系图象如图乙所示.下列说法正确的是( )

| A. | 甲球机械能不守恒,乙球机械能守恒 | |
| B. | 甲、乙两球的质量之比为 m甲:m乙=4:1 | |
| C. | 甲、乙两球的动能均为E k0时,两球重力的瞬时功率之比为 P甲:P乙=1:1 | |
| D. | 甲、乙两球的动能均为E k0时,两球下降高度之比 h甲:h乙=1:4 |
3.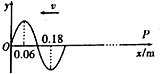 一列向左传播的简谐横波,传播速度大小为v=0.6m/s,t=1.9s时波刚传到O点,波形图如图所示,x轴上的P质点横坐标x=0.96m,则下列说法中正确的是( )
一列向左传播的简谐横波,传播速度大小为v=0.6m/s,t=1.9s时波刚传到O点,波形图如图所示,x轴上的P质点横坐标x=0.96m,则下列说法中正确的是( )
 一列向左传播的简谐横波,传播速度大小为v=0.6m/s,t=1.9s时波刚传到O点,波形图如图所示,x轴上的P质点横坐标x=0.96m,则下列说法中正确的是( )
一列向左传播的简谐横波,传播速度大小为v=0.6m/s,t=1.9s时波刚传到O点,波形图如图所示,x轴上的P质点横坐标x=0.96m,则下列说法中正确的是( )| A. | 图中O质点运动方向沿y轴负方向 | |
| B. | P质点刚开始振动时运动方向沿y轴正方向 | |
| C. | P质点刚开始振动的时间为tP=0.3s | |
| D. | P质点第一次到达波谷的时间为0.6s | |
| E. | P振动的振动周期为0.3s |
10. 如图所示,阻值为R的金属棒从图示位置ab分别以v1、v2的速度沿光滑导轨(电阻不计)匀速滑到a′b′位置,若v1:v2=1:2,则在这两次过程中( )
如图所示,阻值为R的金属棒从图示位置ab分别以v1、v2的速度沿光滑导轨(电阻不计)匀速滑到a′b′位置,若v1:v2=1:2,则在这两次过程中( )
 如图所示,阻值为R的金属棒从图示位置ab分别以v1、v2的速度沿光滑导轨(电阻不计)匀速滑到a′b′位置,若v1:v2=1:2,则在这两次过程中( )
如图所示,阻值为R的金属棒从图示位置ab分别以v1、v2的速度沿光滑导轨(电阻不计)匀速滑到a′b′位置,若v1:v2=1:2,则在这两次过程中( )| A. | 回路电流I1:I2=1:2 | B. | 外力的功率P1:P2=1:2 | ||
| C. | 通过任一截面的电荷量q1:q2=1:2 | D. | 产生的热量Q1:Q2=1:2 |
20. 如图所示,MN、PQ为同一水平面的两平行光滑导轨,导轨间有垂直于导轨平面向里的匀强磁场,导体 ab,cd 与导轨有良好的接触并能滑动,当 ab 沿轨道向右滑动时,cd将( )
如图所示,MN、PQ为同一水平面的两平行光滑导轨,导轨间有垂直于导轨平面向里的匀强磁场,导体 ab,cd 与导轨有良好的接触并能滑动,当 ab 沿轨道向右滑动时,cd将( )
 如图所示,MN、PQ为同一水平面的两平行光滑导轨,导轨间有垂直于导轨平面向里的匀强磁场,导体 ab,cd 与导轨有良好的接触并能滑动,当 ab 沿轨道向右滑动时,cd将( )
如图所示,MN、PQ为同一水平面的两平行光滑导轨,导轨间有垂直于导轨平面向里的匀强磁场,导体 ab,cd 与导轨有良好的接触并能滑动,当 ab 沿轨道向右滑动时,cd将( )| A. | 右滑 | B. | 左滑 | C. | 不动 | D. | 无法确定 |
4. 质量为0.5kg的小物块放在水平地面上的A点,距离A点5m的位置B处是一面墙,如图所示,物块以v0=9m/s的初速度从A点沿AB方向运动,在与墙壁碰撞前瞬间的速度为7m/s,碰后以6m/s的速度反向运动直至静止.碰撞时间为0.05s,g取10m/s2.( )
质量为0.5kg的小物块放在水平地面上的A点,距离A点5m的位置B处是一面墙,如图所示,物块以v0=9m/s的初速度从A点沿AB方向运动,在与墙壁碰撞前瞬间的速度为7m/s,碰后以6m/s的速度反向运动直至静止.碰撞时间为0.05s,g取10m/s2.( )
 质量为0.5kg的小物块放在水平地面上的A点,距离A点5m的位置B处是一面墙,如图所示,物块以v0=9m/s的初速度从A点沿AB方向运动,在与墙壁碰撞前瞬间的速度为7m/s,碰后以6m/s的速度反向运动直至静止.碰撞时间为0.05s,g取10m/s2.( )
质量为0.5kg的小物块放在水平地面上的A点,距离A点5m的位置B处是一面墙,如图所示,物块以v0=9m/s的初速度从A点沿AB方向运动,在与墙壁碰撞前瞬间的速度为7m/s,碰后以6m/s的速度反向运动直至静止.碰撞时间为0.05s,g取10m/s2.( )| A. | 物块与地面间的动摩擦因数μ=0.12 | |
| B. | 墙面对物块平均作用力的大小10 N | |
| C. | 物块在反向运动过程中克服摩擦力所做的功为9J | |
| D. | 碰撞后物块还能向左运动的时间为2s |
5.第一个准确测量出万有引力常量的科学家是( )
| A. | 开普勒 | B. | 第谷 | C. | 牛顿 | D. | 卡文迪许 |
 如图所示,小球Q在竖直平面内做匀速圆周运动,当Q球转到与O同一水平线时,有另一小球P在距圆周最高点为h处开始自由下落,要使两球在圆周最高点相碰,求:
如图所示,小球Q在竖直平面内做匀速圆周运动,当Q球转到与O同一水平线时,有另一小球P在距圆周最高点为h处开始自由下落,要使两球在圆周最高点相碰,求: 如图所示,倾角为θ=30o的光滑斜面上有固定挡板AB,斜面上B、C 两点间高度差为h.斜面上叠放着质量均为m的薄木板和小物块,木板长为L,下端位于挡板AB处,整体处于静止状态.木板和物块两者间的动摩擦因数μ=$\frac{\sqrt{3}}{2}$,最大静摩擦力等于滑动摩擦力.重力加速度为g.
如图所示,倾角为θ=30o的光滑斜面上有固定挡板AB,斜面上B、C 两点间高度差为h.斜面上叠放着质量均为m的薄木板和小物块,木板长为L,下端位于挡板AB处,整体处于静止状态.木板和物块两者间的动摩擦因数μ=$\frac{\sqrt{3}}{2}$,最大静摩擦力等于滑动摩擦力.重力加速度为g.