题目内容
如图所示，一弹簧振子在MN间沿光滑水平杆做简谐运动，O为平衡位置，C为ON中点，振幅A=4cm．从小球经过图中N点时开始计时，到第一次经过C点的时间为0.2s，则小球的振动周期为 s，振动方程的表达式为 cm．
分析：对于简谐运动，从正向最大位移处开始计时，其位移时间关系公式为：x=Acosωt；第一次经过C点的时间为0.2s，代入公式计算出角频率和周期．
解答：解：简谐运动，从正向最大位移处开始计时，其位移时间关系公式为：x=Acosωt；
A=4cm；
0.2s时，x=2cm，代入公式，得到：
2=4cos（ω×0.2）
故ω=
π，T=
=1.2s；
故位移时间表达式为：x=4cos
t；
故答案为：1.2，x=4cos
t．
A=4cm；
0.2s时，x=2cm，代入公式，得到：
2=4cos（ω×0.2）
故ω=
| 5 |
| 3 |
| 2π |
| ω |
故位移时间表达式为：x=4cos
| 5π |
| 3 |
故答案为：1.2，x=4cos
| 5π |
| 3 |
点评：本题关键记住简谐运动的位移时间关系表达式，要能结合位移时间关系表达式求解周期，较难．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
如图所示为一弹簧振子做简谐运动的位移图象，由图象可知该弹簧振子的振幅为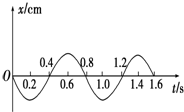
如图所示为一弹簧振子的振动图象，在0～0.8s 时间内，下列说法正确的是（ ）
（2011?静安区二模）如图所示，一弹簧振子在B、C两点间做机械振动，B、C间距为12cm，O是平衡位置，振子每次从C运动到B的时间均为0.5s，则下列说法中正确的是（ ）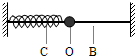
如图所示，一弹簧振子在B、C两点间做机械振动，B、C之间的距离为12cm，O是平衡位置，振子每次从C运动到B的时间均为0.5s，该弹簧振子（ ）
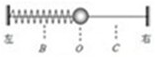如图所示，一弹簧振子沿光滑水平杆在BC间做简谐运动，O为平衡位置，振幅A=6cm．从振子经过图中B点时开始计时，经时间0.1s第一次到达O点，则振子的振动周期T=