题目内容
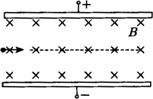
 如图所示,有带电平行板电容器竖直放置,两板之间距离d=0.10m,电势差U=1.0×103V.一个质量为m=0.20g,带正电q=1.0×10-7C的小球用长L=1.0×10-2m的丝线悬挂于电容器内部的O点,现将小球拉到丝线呈水平伸直的位置A,然后无初速释放,假如小球运动到O点正下方B处时,线突然断开,以后发现小球恰能通过B点正下方的C处,试求:
如图所示,有带电平行板电容器竖直放置,两板之间距离d=0.10m,电势差U=1.0×103V.一个质量为m=0.20g,带正电q=1.0×10-7C的小球用长L=1.0×10-2m的丝线悬挂于电容器内部的O点,现将小球拉到丝线呈水平伸直的位置A,然后无初速释放,假如小球运动到O点正下方B处时,线突然断开,以后发现小球恰能通过B点正下方的C处,试求:(1)电容器的左极板带正电荷还是负电荷?
(2)小球运动到C点时的动能EKC为多少?(g取10m/s2)
分析:(1)由线断开后,小球能恰好通过B点正下方的C处,则水平方向先匀减速运动,再向右匀加速运动,所以小球受电场力F水平向右,根据电场力方向和电荷性质判断
左极板带电情况.
(2)若小球摆至B点时丝线突然断裂,小球做曲线运动,运用运动的分解方法:小球水平方向做匀减速直线运动,竖直方向做自由落体运动.
小球由静止释放后到摆到最低点的过程,由动能定理求得小球运动到O点正下方B处时速度.
根据牛顿第二定律求出水平方向加速度,根据对称性和运动学公式求出时间,由竖直方向h=
gt2求出BC相距的距离.
再运用动能定理研究小球从B到C的过程,求出小球运动到C点时的动能.
左极板带电情况.
(2)若小球摆至B点时丝线突然断裂,小球做曲线运动,运用运动的分解方法:小球水平方向做匀减速直线运动,竖直方向做自由落体运动.
小球由静止释放后到摆到最低点的过程,由动能定理求得小球运动到O点正下方B处时速度.
根据牛顿第二定律求出水平方向加速度,根据对称性和运动学公式求出时间,由竖直方向h=
| 1 |
| 2 |
再运用动能定理研究小球从B到C的过程,求出小球运动到C点时的动能.
解答:解:(1)由线断开后,小球能恰好通过B点正下方的C处,则水平匀减速运动,竖直在重力作用下自由落体运动.
∴小球受电场力F水平向右,左极板应带正电.
(2)小球由静止释放后到摆到最低点的过程,由动能定理得
mgL-EqL=
mvB2
又E=
,
代入解得vB=
m/s
小球摆至B点时丝线突然断裂,小球水平方向做匀减速直线运动,加速度大小为
a=
=5m/s2
根据对称性t=
=
s
小球在竖直方向做自由落体运动,则 h=
gt2
代入解得h=
m.
运用动能定理研究小球从B到C的过程,
mgh=EkC-EkB
EKC=mgh+EkB=2×10-4×10×
+
×2×10-4×(
)2=1.7×10-4 J
答:(1)电容器的左极板带正电荷.
(2)小球运动到C点时的动能EKC为1.7×10-4 J.
∴小球受电场力F水平向右,左极板应带正电.
(2)小球由静止释放后到摆到最低点的过程,由动能定理得
mgL-EqL=
| 1 |
| 2 |
又E=
| U |
| d |
代入解得vB=
| ||
| 10 |
小球摆至B点时丝线突然断裂,小球水平方向做匀减速直线运动,加速度大小为
a=
| Eq |
| m |
根据对称性t=
| 2v |
| a |
| ||
| 25 |
小球在竖直方向做自由落体运动,则 h=
| 1 |
| 2 |
代入解得h=
| 2 |
| 25 |
运用动能定理研究小球从B到C的过程,
mgh=EkC-EkB
EKC=mgh+EkB=2×10-4×10×
| 2 |
| 25 |
| 1 |
| 2 |
| ||
| 10 |
答:(1)电容器的左极板带正电荷.
(2)小球运动到C点时的动能EKC为1.7×10-4 J.
点评:本题是电场中力学问题,采用的是力学的方法处理,关键是分析物体的受力情况和运动情况,选择解题规律.
选取研究过程,运用动能定理解题.动能定理的优点在于适用任何运动包括曲线运动.
选取研究过程,运用动能定理解题.动能定理的优点在于适用任何运动包括曲线运动.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
 如图所示,两块平行、正对的金属板水平放置,分别带有等量的异种电荷,使两板间形成匀强电场,两板间的距离为d.有一带电粒子以某个速度v0紧贴着A板左端沿水平方向射入匀强电场,带电粒子恰好落在B板的右边缘.带电粒子所受的重力忽略不计.现使该粒子仍从原位置以同样的方向射入电场,但使该粒子落在B板的中点,下列措施可行的是( )
如图所示,两块平行、正对的金属板水平放置,分别带有等量的异种电荷,使两板间形成匀强电场,两板间的距离为d.有一带电粒子以某个速度v0紧贴着A板左端沿水平方向射入匀强电场,带电粒子恰好落在B板的右边缘.带电粒子所受的重力忽略不计.现使该粒子仍从原位置以同样的方向射入电场,但使该粒子落在B板的中点,下列措施可行的是( )| A、仅使粒子的初速度变为2v0 | ||
B、仅使粒子的初速度变为
| ||
C、仅使B板向上平移
| ||
| D、仅使B板向下平移d |
 如图所示,在两平行边AB CD的狭长区域内,分布有磁感应强度B=1T而方向垂直纸面向外的匀强磁场,磁场区域宽度d=2cm.一带正电的粒子,质量m=3.2×10-27kg,带电量q=1.6×10-19Cv,以速v=2×106m/s从左边界的O处斜向上射入磁场,粒子刚好从另一边界垂直射出,求:
如图所示,在两平行边AB CD的狭长区域内,分布有磁感应强度B=1T而方向垂直纸面向外的匀强磁场,磁场区域宽度d=2cm.一带正电的粒子,质量m=3.2×10-27kg,带电量q=1.6×10-19Cv,以速v=2×106m/s从左边界的O处斜向上射入磁场,粒子刚好从另一边界垂直射出,求: 如图所示,有一带电粒子进入电场沿曲线AB运动,虚线a,b,c,d为电场中的等差等势面,且Ua>Ub>Uc>Ud,粒子在A点初速度V0的方向与等势面平行.不计粒子的重力,下面说法正确的是( )
如图所示,有一带电粒子进入电场沿曲线AB运动,虚线a,b,c,d为电场中的等差等势面,且Ua>Ub>Uc>Ud,粒子在A点初速度V0的方向与等势面平行.不计粒子的重力,下面说法正确的是( ) 如图所示,有三个质量相等,分别带正电,负电和不带电的小球,从上、下带电平行金属板间的P点.以相同速率垂直电场方向射入电场,它们分别落到A、B、C三点,则( )
如图所示,有三个质量相等,分别带正电,负电和不带电的小球,从上、下带电平行金属板间的P点.以相同速率垂直电场方向射入电场,它们分别落到A、B、C三点,则( )